planimetria
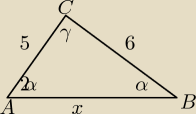
pic: W trójkącie ABC dane są długości dwóch boków 5 i 6. Stosunek miar kątów leżących naprzeciwko
tych boków jest równy 1:2. Wyznacz długość trzeciego boku trójkąta.
Zrobiłem sobie rysunek.
|< ABC| = α
|< CAB| = 2 α
|< ACB| = γ
|AC| = 5
|BC| = 6
|AB| = x
Dalej niestety nie wiem co zrobić. Proszę o pomoc.
Pozdr.
12 lut 16:45
Mila:
z tw. sinusów
| 6 | | 5 | | 3 | |
| = |
| ⇔cosα= |
| |
| 2sinαcosα | | sinα | | 5 | |
z tw. cosinusów
5
2=x
2+6
2−2x*6*cosα
dokończ
12 lut 17:30
pic: Właśnie doszedłem do tego samego.
i wychodzą dwie odpowiedzi:
x
2 = 5
Jaką odrzucić i dlaczego? Bo w odpowiedziach jest tylko jedna...
12 lut 18:01
Mila: rozważ przypadki
x=5, to Δ jest równoramienny
γ=α, 4α=180
2α=90
α=45 wnioski?
12 lut 18:30
pic: Czyli byłby to trójkąt prostokątny o przyprostokątnych 5 i przeciwprostokątnej 6, co jest
niemożliwe. Ok. Dzięki wielkie!
12 lut 18:42
Mila: 
12 lut 19:02