funkcje i ich własności sylw.: dana jest funkcja określona wzorem f(x)=|x+6|−2|x|+|x+3| x∊(−6;0) a) zapisz wzór tej funkcji bez użycia symbolu wartości bezwzględnej b) narysuj wykres tej funkcji c) podaj zbiór wartości funkcji f bardzo proszę nie tylko o rozwiązanie ale i wytłumaczenie punktu a

tim : Odpowiedz na pytanie: Wg wartości bezwglęgnej: { x |x| = { − x Czyż nie?

sylw.: czyli jak to będzie?

Bogdan: f(x)=|x + 6| − 2|x| + |x + 3| Dla x ∊ (−∞, −6): f(x) = −x − 6 + 2x − x − 3 ⇒ f(x) = −9 Dla x ∊ <−6, −3): f(x) = x + 6 + 2x − x − 3 ⇒ f(x) = 2x + 3 Dla x ∊ <−3, 0): f(x) = x + 6 + 2x + x + 3 ⇒ f(x) = 4x + 9 Dla x ∊ <0, +∞): f(x) = x + 6 − 2x + x + 3 ⇒ f(x) = 9 Odp.: Dla x ∊ (−6, 0): {2x + 3 dla x ∊ <−6, −3) f(x) = { {4x + 9 dla x ∊ <−3, 0) (powinna być jedna klamra)

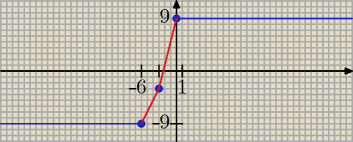
Bogdan: Kolorem czerwonym zaznaczyłem tę część wykresu funkcji f(x), która zawarta jest w przedziale x ∊ (−6, 0). Zbiór wartości funkcji dla x ∊ (−6, 0): ZW_f: y ∊ (−9, 9). To wszystko