Narysować zbiór na płaszczyźnie zespolonej
Tomek: To zadanie zaczyna mnie już straszyć po nocach. Wiem, że jego rozwiązanie jest proste, ale nie
mogę na nie wpaść.
Powinno mi wyjść równanie okręgu.
Dochodzę do czegoś takiego i dalej kiszka (coś mi nie gra w tym rozwiązaniu):
Do czegoś takiego doszedłem jak zastąpiłem z przez x+iy, a potem zacząłem pozbywać się i z
mianownika. Mniej więcej tak:
| | (1−x+iy)(1+x−iy) | |
Re[ |
| ]=1 |
| | (1+x+iy)(1+x−iy) | |
A i bardziej niż sam wynik interesuje mnie jak do takich zadań podchodzić.
12 lut 12:13
Tomek: Nie chciałbym być upierdliwy, ale zależy mi, żeby to ogarnąć.

12 lut 14:41
panteon: te nawiasy to moduł czy nawias?
12 lut 14:42
Tomek: Nawias.
12 lut 14:43
panteon: najpierw podstawiasz za z potem dzielisz to co w nawiasie, potem z tego co wyjdzie wyciągasz
samą część rzeczywistą i masz równanie które przekształcasz ewentualnie.
12 lut 14:50
Tomek: Co ja mam podzielić, bo nie rozumiem. Mam pozbyć się urojonej z mianownika?
12 lut 14:58
panteon: tak, po za tym chyba to robiłeś tylko źle troche w ty równaniu które napisałeś jako drugie w
liczniku powinno być − y2 i wtedy rzeczywiście wychodzi okrąg
12 lut 15:01
Tomek: Ok. Błąd robiłem tutaj −z to −x−iy, a nie −x+iy.

Teraz tylko pomyślę jak to przenieść na wykres. Dzięki wielkie.

12 lut 15:14
Mila:
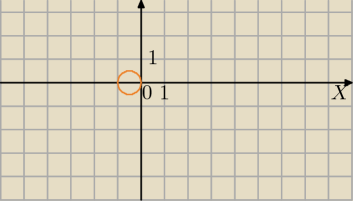
12 lut 16:41
panteon: | | 1 | | 3 | |
a nie : (x+ |
| )2 + y2 = |
| |
| | 2 | | 4 | |
12 lut 18:12

 Teraz tylko pomyślę jak to przenieść na wykres. Dzięki wielkie.
Teraz tylko pomyślę jak to przenieść na wykres. Dzięki wielkie. 
