planimetria Overplay: Miara jednego z kątów trójkąta jest równa 30 st. Pole tego trójkąta wynosi √3, a promień okręgu opisanego jest równy 2. Oblicz promień okregu wpisanego w ten trójkąt.

Overplay: jedynie co to z tw sin wychodzi mi ze bok naprzeciw kata 30st ma dlugosc 2 i nie wiem co dalej

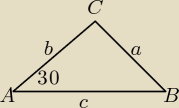
Mila: a=2 to policzyłeś, potrzebne są jeszcze boki aby skorzystać z wzoru

	1
P=		(a+b+c)*r, gdzie r− promień okręgu wpisanego
	2

	1
P=		bc*sin30=√3
	2

bc=4√3 z tw. cosinusów a²=b²+c²−2bccos30

	√3
22=b2+c2−2*4√3*
	2

4=b²+c²−12 b²+c²=16 bc=4√3 masz uklad, rozwiąż. Może jest inny łatwiejszy sposób.