pilne darkcarmell: Zad 1Średnicę okręgu o środku O jest bok AB trójkąta ABC. Okrag ten przecina bok Ac w punkcie D i bok BC w punkcie E. Wiedząc że AB=15cm BE=9cm,CE=5cm oblicz DC i AD Zad 2 W trójkącie ABC środkowe poprowadzone z wierzchołków A i B są do siebie prostopadłe. Wykaż, że jeżeli BC=a, AC=b, AB= 2√^a2+b2₅

Eta: 1/ z tw. Pitagorasa w ΔABE |AE|²= 15²−9² ⇒ |AE|= 12 w ΔACE |AC|²= 12²+5² ⇒ |AC|= 13 |AC|= |AD|+|DC|= y+z= 13 |DB|=x z tw. Pitagorasa y²=15²−x² i z²=14²−x² odejmując te równania stronami otrzymasz :

	29
z2−y2= 29 ⇒ (z+y)(z−y)=29 ⇒ 13(z−y)=29 ⇒ z−y=
	13

	29
rozwiąż układ równań: z−y=
	13

z+y= 13 otrzymasz : |AD|=y=.... |DC|=z=.....

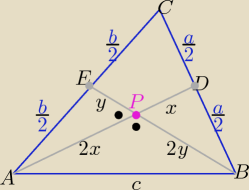Eta: 2/ środkowe w trójkącie dzielą się w stosunku 2:1 licząc od wierzchołka to: |AP|=2x , |PD|=x , x>0 i |BP|=2y , |PE|=y, y>0 i teraz z tw. Pitagorasa (2x)²+(2y)²= c² ⇒ 4(x²+y²)= c²

	b		a
(*) (2x)2+y2= (		)2 i (**)(2y)2+x2= (		)2
	2		2

dodając stronami (*) i (**)

	a2		b2		a2+b2
5x2+5y2=		+		⇒ 5(x2+y2)=
	4		4		4

	5*c2		a2+b2		a2+b2
to:		=		⇒ c= |AB|= √
	4		4		5

c.n.u

darkcarmell: bardzo bardzo bardzo bardzo dziękuję

dasd: