kąt Seba_xD: Uzasadnij, że kąt między krawędzią i przekatną sześcianu ma miarę mniejszą niż 55⁰.

Seba_xD: pomoże mi ktoś ?

Dominik: jest rysunek?

Aga1.:

	d		a√2
tgα=		=		=√2
	a		a

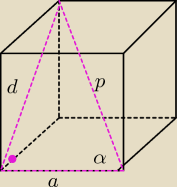
teraz wystarczy skorzystać z tablic.

PW: Narysuj kąt α, o którym mówi zadanie i zauważ, że przekątna sześcianu, krawędź i przekątna ściany bocznej tworzą trójkąt prostokątny (tego na rysunku nie widać, ale wynika z twierdzenia o trzech prostopadłych − krawędź w podstawie jest prostopadła do dwóch krawędzi ściany bocznej, a więc i do jej przekątnej). Z definicji tangensa jest więc

	√2a
tgα =		= √2
	a

"a" to krawędź sześcianu, a√2 − długośc przekątnej ściany bocznej (ta przekątna jest przyprostokątną rozważanego trójkąta) W tablicach sprawdzasz, że tg55°>√2, czyli tg55°>tgα i z faktu, że tg jest funkcją rosnącą na

	π
(0,		) wynika 55°>α.
	2

PW: Aga1: Właśnie tego rysunku było brak (a nie cierpię tu rysować), mamy komplet, dziękuję.

Seba_xD: Dzięki, teraz zadanie się wydaje proste, bo praktycznie nie trzeba nic liczyć. Tylko gorzej jest niestety wpaść na takie coś

Aga1.: Witaj PW, ja z kolei nie lubię dużo pisać.

PW: Aga1 ,. Śmiałem się, aż rodzina podejrzliwie na mnie zaczęła spoglądać − oczywiście dla siebie zrobiłem rysunek − był identyczny jak Twój, łącznie z oznaczeniami i wybranym "rogiem", a przecież tego nie widziałem pisząc swoje rozwiązanie.

Aga1.: Może jestem Twoim uczniem.

PW: A miałaś nauczyciela matematyka o inicjałach "PW"? Są prawdziwe.