planametria pwl: Trójkąt prostokątny ma przyprostokątne długości a i b, a wysokość opuszczona na przeciwprostokątną ma długość h. Wykaż że 1/h²=1/a²+1/b²

Dominik: a² + b² = c²

	ch		√a2 + b2h
P =		=
	2		2

	ab
P =
	2

√a² + b²h = ab

	1
(a2 + b2)h2 = (ab)2 /*
	h2a2b2

1		a2 + b2
	=
h2		(ab)2

	1		1
i dalej nie mam pomyslu. z wolframa, wiem, ze prawa strona wynosi		+		, ale
	a2		b2

jak to udowodnic? od biedy mozna sprawdzic tozsamosc.

OMG:

1		1		1
	=		+
h2		a2		b2

1		a2 + b2
	=
h2		(ab)2

1		c2
	=
h2		(ab)2

(ab)² = (ch)² ab = ch

	ab
h =
	c

Można zauważyć, że:

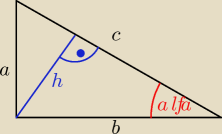
a		h
	= sinα i		= sinα
c		b

a		h
	=
c		b

hc = ab

	ab
h =
	c

Co należało udowodnić.

OMG: Oczywiście podstawiając teraz za c z powrotem a² + b² otrzymamy pierwotną równość.

Ajtek: Rozbij to na dwa ułamki po prawej stronie .

OMG: Tylko trzeba wpierw podnieść stronami do kwadratu bo c² = a² + b²

Dominik: @Ajtek, no przeciez! strasznie nieogarniety dzis jestem.

1		a2 + b2
	=
h2		a2b2

1		a2		b2
	=		+
h2		a2b2		a2b2

1		1		1
	=		+
h2		a2		b2

cnw

Eta: