matematykaszkolna.pl
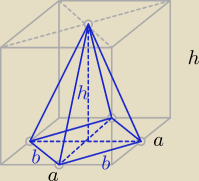
Proszę o pomoc Gosia : Środek górnej podstawy graniastosłupa prawidłowego czworokątnego i środki krawędzi jego dolnej podstawy są wierzchołkami ostrosłupa wpisanego w ten graniastosłup. Oblicz stosunek objętości tego ostroslupa do objętości graniastoslupa
10 lut 17:04
Gosia : ?
10 lut 17:40
dero2005: rysunekVg = a2*h
 a√2 
b = √(a2)2 + (a2)2 =
 2 
 b2*h a2*h 
Vo =
=
 3 6 
Vo 
a2*h 
6 
 1 
=
=
Vg a2*h 6 
10 lut 18:56
Gosia : nie rozumiem
10 lut 18:57
dero2005: co konkretnie?
10 lut 19:01
Gosia : b=
10 lut 19:08
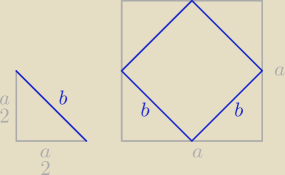
dero2005: rysunek (a2)2 + (a2)2 = b2 a24 + a24 = b2
2a2 
= b2
4 
a2 
= b2
2 
 a a√2 
b =
=
 √2 2 
10 lut 19:24
Gosia : i jeszcz Vo
10 lut 19:25
dero2005: Vo − objętość ostrosłupa wzór na objętość ostrosłupa to jest iloczyn pola podstawy i wysokości podzielony przez 3 a więc pole podstawy ostrosłupa = a2 objętość więc wyniesie
 b2*h 
Vo =
 3 
 a√2 
teraz wstawiamy za b =
 2 
 
 a√2 
(
)2*h
 2 
 
2a2 
*h
4 
 a2*h 
Vo =
=
=
 3 3 6 
10 lut 19:33
Gosia : aha dzięki
10 lut 19:35
dero2005: pole podstawy ostrosłupa = b2 a nie a2 jak błędnie napisałem powyżej
10 lut 19:36