Zadanka. tim : Witam. Teraz ja dodam kilka wakacyjnych zadanek , może chociaż ciut zmuszą was do dłuższego intensywnego myślenia, a nie, że hop siup i gotowe . A więc: 1. Wiadomo, że liczba 35! jest równa: 10333147966386144929x66651337523200000000, gdzie x jest nieznaną cyfrą. Znajdź x. 2. Rozwiąż układ równań: { x² + y² + z² = 3 { xy + xz + yz = 3 3. O liczbach naturalnych a, b, c, d, f wiadomo, że:

a		c		e
	>		>		oraz af − be = 1
b		d		f

Wykaż, że d ≥ b + f Na razie tyle

Basia: Witaj Timuś ! 1 i 2 są w gruncie rzeczy łatwe. Mam napisać rozwiązanie albo wskazówki czy sam "pogłówkujesz" ? Na 3 nie mam na razie pomysłu.

Jakub: Witam Tim, Basia! Do drugiego zadania podpowiem tylko, że wzory skróconego mnożenia się przydadzą.

Basia: Witaj Jakubie ! Oczywiście, stare, dobre wzory zawsze się przydają. Tu również. Innego sposobu właściwie nie widzę.

Basia: Podpowiedź do 1. 35! musi być liczbą podzielną m.innymi przez 3 i 9.

AS: ad zad 1. Najprościej wyliczyć 35! i porównać. A tak na marginesie 35! jest podzielne przez wszystkie liczby naturalne od 1 do 35.i ich kombinacje iloczynowe. ad zad 2. (x + y + z)² = x² + y² + z² + 2*(x*y + x*z + y*z) (x + y + z)² = 3 + 2*3 = 9 Stąd x + y + z = ± 3 Rozwiązać należy układ równań x + y + z = ± 3 x² + y² + z² = 3 x*y + x*z + y*z = 3 Rozwiązaniami są liczby: x = y = z = 1 lub x = y = z = −1 Nad rozwiązaniem układu jeszcze pogłówkuję.

Basia: Ad.1 Suma cyfr liczby podzielnej przez 9 jest podzielna przez 9. Z tego wynika, że x=2 (o ile nie pomyliłam się w dodawaniu; wyszło mi 52), bo z liczb 52+x gdzie x=1,2,...,9 tylko 54 jest podzielna przez 9. Liczenie 35! jest zbyteczne Ad.2 (x+y+z)² = x²+y²+z²+2xy+2xz+2yz = (x²+y²+z²)+2(xy+xz+yz) = 2+2*3=9 stąd x+y+z=3 lub x+y+z=−3 x+y+z=3 jest równaniem płaszczyzny wyznaczonej przez punkty A(1,0,0) B(0,1,0) C(0,0,1) x+y+z=−3 jest równaniem płaszczyzny wyznaczonej przez punkty A(−1,0,0) B(0,−1,0) C(0,0,−1) ten układ równań ma nieskończenie wiele rozwiązań

AS: Coś nie mogę się połapać. Zgadzam się,że równanie x + y + z = 3 ma nieskończenie wiele rozwiązań ale czy spełniają pozostałe dwa pozostałe równania tj. x² + y² + z² = 3 x*y + x*z + y*z = 3? Odnośnie zad.1 dlaczego 9 jest tak uprzywilejowana, skoro jest jeszcze tyle innych dzielników? A np. dlaczego nie 3?

♊: AS: zadanie pierwsze: ponieważ tylko cyfry 3 i 9 mają takie przydatne własności. Jeżeli coś jest podzielne przez 9 to jest tez podzielne przez 3, ale w 2gą strone to nie działa do końca − jest 3 razy więcej przypadków (i przez 3 podzielne powinny być liczby dla x ∊ {2,5,8}) Basiu − tam na końcu powinnaś otrzymać 3+2*3. Wydaje mi sie też, że Twoim sposobem umknęły Ci niektóre ograniczenia odnośnie zadania, ale pewny nie jestem.

Basia: ad1. Oczywiście 3+2*3 dlatego = 9 (literówka). ad.2 Nie umknęły ad.AS ten układ równań i równanie (x+y+z)²=9 są równoważne x²+y²+z²=3 xy+xz+yz=3 x²+y²+z²=3 2xy+2xz+2yz=6 −−−−−−−−−−−−−−−−−−−−−−−−−−−− x²+y²+z²+2xy+2xz+2yx=9 (x+y+z)²=9 x+y+z=3 lub x+y+z=−3 rozwiązaniem jest każda trójka liczb, które są współrzędnymi jednego z punktów płaszczyzny ABC gdzie A(1,0,0) B(0,1,0) C(0,0,1) i każda trójka liczb, które są współrzędnymi jednego z punktów płaszczyzny DEF gdzie D(−1,0,0) E(0,−1,0) F(0,0,−1)

Bogdan: Dzień dobry. Tim, udało Ci się, tym razem, nie nastąpiło "hop siup i gotowe", trzeba przy Twoich zadaniach dłużej pogłówkować. Ad. 1. Liczba 35! dzieli się oczywiście przez wszystkie dodatnie liczby całkowite od 1 do 35 (włącznie), w tym oczywiście dzieli się przez 9. Suma cyfr liczby 35! wynosi 138, ta liczba dzieli się przez 3, ale nie dzieli się przez 9. Jedyną liczbą, która zwiększa 138 do liczby podzielnej przez 9 jest 6 (138 + 6 = 144 = 9*16). Odp.: W miejsce x trzeba wstawić 6. Łatwo to sprawdzić przy pomocy komputerowego kalkulatora. Ad. 2. Układ równań: 1. { x² + y² + z² = 3 2. { xy + xz + yz = 3 Klamry oznaczają zamknięcie równań w układ równań. Przeprowadźmy takie rozumowanie (proszę o ewentualne poprawienie): Po obustronnym wymnożeniu równania xy + xz + yz = 3 przez 2 i następnie po dodaniu równań otrzymujemy (co wszyscy stwierdziliście) : x² + y² + z² + 2xy + 2xz + 2yz = 9 ⇒ (x + y + z)² = 9, stąd mamy równanie nr 3: 3. x + y + z = 3 lub x + y + z = −3. Pytanie: Czy jest teraz układ trzech równań, czy nadal dwóch? Myślę, że nadal mamy układ dwóch równań, bo równanie nr 3 powstało w wyniku działań wykonanych na równaniach nr 1 i 2. Można więc pierwotny układ równań przedstawić w postaci układu równań nr 1 i 3 lub 2 i 3. Zbudujmy układ równań z równań 2 i 3: a) 2. { xy + xz + yz = 3 lub b) 2. { xy + xz + yz = 3 3. { x + y + z = 3 3. { x + y + z = −3 Ad. a) 2. z(x + y) = 3 − xy 3. z = 3 − (x + y) 2. (3 − (x + y))(x + y) = 3 − xy ⇒ 3(x + y) − (x + y)² = 3 − xy ⇒ ⇒ 3x + 3y − x² − 2xy − y² = 3 − xy ⇒ x² + (y − 3)x + (y² − 3y + 3) = 0 Potraktujmy ostatnie równanie jak równanie kwadratowe z niewiadomą x i parametrem y. Δ = y² − 6y + 9 − 4y² + 12y − 12 = −3y² + 6y − 3 = −3(y² − 2y + 1) = −3(y − 1)² Δ ≥ 0 ⇔ y = 1, wtedy Δ = 0 Jeśli y = 1, to równanie kwadratowe x² + (y − 3)x + (y² − 3y + 3) = 0 przyjmuje postać: x² −2x + 1 = 0 ⇒ (x −1)² = 0 ⇒ x = 1. z = 3 − (x + y) ⇒ z = 3 − (1 + 1) = 1 Otrzymaliśmy więc dla przypadku a), w którym x + y + z = 3 jedno rozwiązanie: x = y = z = 1 Podobnie rozpatrzeć można przypadek b), w którym x + y + z = −3 Jeszcze uwaga na koniec. Rozwiązanie musi spełniać równanie płaszczyzny: x + y + z = 3 i powierzchni xy + xz + yz = 3 lub x + y + z = −3 i xy + xz + yz = 3.

tim : Bogdanie, miło mi, że się udało <yeah!>. Trochę się rozpisałeś, ale ja rozwiązałem t trochę łatwiej i inaczej: x² + y² + z² = 3 xy + xz + yz = 3 Przyrównujemy: x² + y² + z² = xy + xz + yz /*2 x² + x² + y² + y² + z² + z² = 2xy + 2xz + 2yz Teraz wystarczy przenieść i pogrupować: x² − 2xy + y² + x² − 2xz + z² + y² − 2yz + z² = 0 Widzicie już (Jakub miał racje )... Po przekształceniach zostaje: x = y = z... Podstawiamy do układu równań i zostaje: x = y = z = 1 lub x = y = z = −1

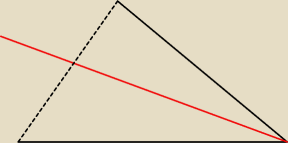
tim : A ja mam pytanie co do dwusiecznej. Jeżeli dwusieczna (czerwona) kąta przecina bok trójkąta, to czy dzieli go na pół?

Bogdan: A znasz twierdzenie o dwusiecznej w trójkącie?

Bogdan: Odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku to środkowa. Czy środkowa to to samo, co dwusieczna?

Bogdan: Patrz 498

AS: A czy dwusieczna kąta może nie dzielić bok trójkąta?

tim : AS: Tak, jeżeli poprowadzimy dwusieczną kąta wypukłego . Bogdan: Dzięki, bo nie byłem pewien, rysowałem i rysowałem i za każdym razem mi się prawie pokryło..

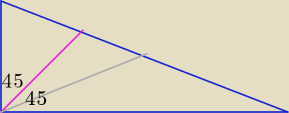
Bogdan: Tim, dobrze to widać na trójkącie prostokątnym nierównoramiennym z dwusieczną wyprowadzoną z wierzchołka kąta prostego, różowym kolorem oznaczyłem dwusieczną, szarym − środkową.

tim : Zabrałem się za rozwiązywanie zadań z książki: "Zadania z matematyki dla olimpiczyków" tzw. krowa i tam są zadania głównie na udowodnij, że z którymi rzadko się dotychczas spotykałem i sprawiają mi trudność. A i jeszcze jedno czy x² (dowolny x) może mieć na końcu trzy zera?

tim : (sprecyzuję x ∊ całkowitych)

b.: może, np. 100²=10000 ma na końcu 3 zera

b.: ale dokładnie 3 zer mieć nie może −− wystarczy popatrzeć na podzielność przez 2 i 5...

tim : Pomysłowa odpowiedź "może, np. 1002=10000 ma na końcu 3 zera" ^^. Ale chodziło o to drugie.

AS: a może x² = 100⁰

tim : x² = 1000, dla x = √1000, więc nie całkowite

tim : A tak wgl to witaj AS

tim : Nstp pytanie z serii udowodnij, że: Mam zadanie (cytat): "Wykaż że dla dodatnich liczb x, y, z, a (x, y, z, a ∊ R) prawdziwe jest równanie" To mam wykazać: a. że prawdziwe jest dla dodatnich (przyjąć na początku, że są dodatnie i sprawdzić czy wyjdzie prawda) czy, b. że jest prawdziwe tylko dla dodatnich (rozwiązać i odpowiednio przekształcić wynik by udowodniż, że dla dodatnich). b. że jest prawdziwe dla dodatnich i nieprawdziwe dla ujemnych.. Które

♊: tim! ale jakie równanie ?

tim : Tzn mnie interesuje sama idea , równanie jest najmniej ważne.. Chodzi o to, że: mam polecenie: Wykaż, że dla dodatnich liczb x, y, z, a (rzeczywiste) prawdziwe jest równanie..." I teraz, czy mogę od razu przyjąć, że x, y, z, a są dodatnie i wykazać że wychodzi poprawny wynik. Czy muszę pisać i tak modułować równanie, żeby wyszło że jest prawdziwe dla dodatnich...

♊: tim − są różne metody. Możesz załozyć, że twierdzenie nie zachodzi dla dodatnich i doprowadzić do sprzeczności. Mozesz też założyć, że są dodatnie (nawet powinieneś).

tim : Tzn mam wykazać, że zachodzi dla dodatnich, więc zakładam tak na początku, tak? Do sprzeczności nie mogę (gdyż zapewne dla niektórych ujemnych również zachodzi).