równanie okręgu 123: Znajdź równanie okręgu opisanego na trójkącie ABC o wierzchołkach A=(5,5) B=(−2,4) C=(−1−3).

123: te punkty mam podstawic do wzoru : (x−a)²+(y−b)²=r²? Mam jeszcze jedno pytanie, jak wylicze r po podstawieniu do tego równania?

Eta: równanie ma postać: x² +y² −2ax −2by +c =0 gdzie : S(a,b) r= √a² +b² −c podstaw współrzędne każdego z punktów, otrzymasz układ trzech równań z a, b , c rozwiąż ten układ i oblicz a , b , c dalej już prosto Powodzenia!

Eta: Może też tak być , jak napisałeś. otrzymasz układ trzech równań, tym razem z a, b, r Policz a, b , r ...... i to wszystko

123: Dziękuję. Mam jeszcze ostatnie zadanie z tego zakresu, jakbyś mogła Eto podac jakies wskazówki byłbym bardzo Ci wdzięczny. Punkty A=(0,−1) i B=(−2,1) należą do okręgu x²+y²−2x−4y−5=0. Wyznacz współrzędne takiego punktu C należącego do okręgu by trójkąt ABC był trójkątem równoramiennym o podstawie AB.

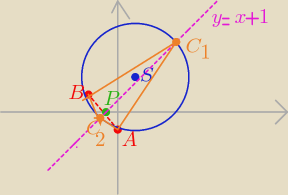
Eta: Witam Sorry , nie było mnie przez chwilę. odp: do zad1/ a= 2 b= 1 r=5 (x−2)² + ( y−1)² = 25 zad2/ wyznacz środek S tego okręgu ( potrafisz z pewnością ( x −1)² + ( y −2)² = 10 => S( 1, 2) następnie oblicz współrzędne P −− środka odcinka AB napisz równanie prostej PS rozwiązując układ równań tej prostej z tym okręgiem otrzymasz współrzędne punktu C ( będą dwa takie punkty)

Eta:

Eta: ΔABC₁ i Δ ABC₂ −−−− są równoramienne

Eta: odp: C₁( 1 + √5 , 2 +√5) C₂( 1 − √5, 2 − √5)

123: Mnie również nie było − byłem na zajęciach z angielskiego. Dziękuję za fatygę,biorę się za rozwiązywanie