Kilka zadanek na dowodzenie Squall: Witajcie kochani. Wrzucę kilka prostych zadanek. Jeśli ktoś chce się sprawdzić to zapraszam do rozwiązywania 1) Udowodnij, że różnica kwadratu pewnej liczby naturalnej i tej liczby jest liczbą parzystą 2) Korzystając z zasady indukcji matematycznej udowodnij, że jeśli dla dowolnej liczby

	n(n+1)
naturalnej zachodzi równość: 1+2+...+n=
	2

	n k		n k+1		n+1 k+1
3) Udowodnij, że:		+		=

Squall: ad.2: bez "jeśli"

Mariusz: zad 1 x²−x= x(x−1) iloczyn dwóch kolejnych liczb jest zawsze podzielny przez 2 − czyli jest liczbą parzystą Zad 2

	n(n+1)
Z: 1+2+3....+n=
	2

	(n+1)(n+2)
T: 1+2+3.....+n+n+1=
	2

Dowód

	(n+1)(n+2)
1+2...+n=		−n−1
	2

	n(n+1)
1+2+3....+n=		cnu.
	2

Squall: ad.1 − zadanie pierwsze − ok. Później podam jeszcze inny sposób (chyba, że ktoś jeszcze spróbuje) ad.2 − ok Zadanie 3 wciąż czeka na rozwiązanie

Mariusz: ad 1 też można z indukcji nad trzecim musze pomyśleć, postaram się wieczorem podać rozwiązanie

AS: Mam zastrzeżenia do dowodu zad.2 podanego przez Mariusza. W zasadzie wykazał że zachodzi założenie a nie że zachodzi również dla n = k + 1 Oto moja propozycja: Krok 1 n = 1 1 = 1 Krok 2 n = k 1 + 2 + ... + k = k*(k + 1)/2 Krok 3 N = k + 1 k*(k + 1) (k + 1) + 2*(k + 1) 1 + 2 + ... + k + (k + 1) = −−−−−−− + (k + 1) = −−−−−−−−−−−−−− = 2 2 (k + 1)*(k + 2) N *(N +1) −−−−−−−−−−− = −−−−−−− 2 2 c.n.d.

Mariusz: Asie wydaje mi się że mamy napisane to samo tylko że ja użyłem oznaczeń n zamiast k. Jeżeli nie przeniósłbym n+1 na drugą stronę to otrzymałbym to samo Oczywiście zgadzam się z twoim dowodem. Brakuje mi tylko w jednym miejscu k

k*(k+1)		k*(k+1)+2(k+1)
	+k+1=
2		2

Bogdan: Nie wdając się w polemikę, powiem, że osobiście wolę stosować 4 kroki wyraźnie je nazywając, co pozwala uniknąć nieporozumień. 1. Sprawdzenie dla n = 2:

	2*3
1 + 2 =		⇒ 3 = 3, czyli L = P.
	2

2. Założenie dla n= k:

	k*(k + 1)
1 + 2 + ... + k =
	2

3. Teza dla n = k + 1:

	(k + 1)(k + 2)
1 + 2 + ... + k + (k + 1) =
	2

4. Dowód:

	k*(k + 1)		k*(k + 1)		2(k + 1)		(k + 1)(k + 2)
		+ (k + 1) =		+		=
	2		2		2		2

cnd. Podobnie został przeprowadzony ten dowód na stronie: http://pl.wikibooks.org/wiki/Matematyka_dla_liceum/Ci%C4%85gi_liczbowe/Rekurencja_i_indukcja_matematyczna

Bogdan: W zadaniu 3 wystarczy każde z wyrażeń rozpisać zgodnie z definicją symbolu Newtona i sprowadzić lewą stronę do wspólnego mianownika.

AS: Z natury swej jestem zgodnym człowiekiem. Przedstawiam swój pogląd,swoje stanowisko, a ktoś może mieć inne. Zasada indukcji matematycznej wyraźnie wskazuje kolejność dowodzenia 1 → n → n + 1 i oto mi chodziło by ostatnie wyrażenie było przedstawione w postaci W(n + 1). Ale jak ktoś ma inny pogląd to ja mu tego nie bronię.

Mariusz: może żeczywiście zapisałem to troche nie dokładnie Ale napewno zarówno Ty jak i Bogdan macie racje. Cieszę się że mogę się uczyć wielu ciekawych metod od was

Eta: Zad1 Dane są: x= (10)^{1_{1− logz}} y=(10)^{1_{1− logx}} wykaż,że : z= (10)^{1_{1 −logy}} PS: 10 −−−− to podstawa potęgi ...... zaś cały ułamek jest wykładnikiem tej potęgi.

Eta: zad2 Spośród trójkątów o wierzchołkach: A( m −2 , m −2) , B( m +2, − 4) , C( 3, − m) wybierz ten ,który ma kąt prosty przy wierzchołku C i pole równe 6[j²]. Dla wybranego trójkąta napisz równania prostych w których zawierają się jego boki .

Bogdan: Co za czasy przyszły, że sami sobie zadania zadajemy. Też Eto przed chwilą zastanawiałem się, czy nie wrzucić tu dzisiaj jakiegoś zadanka, bo nudno się zrobiło

Eta: Witam Bogdanie. Wakacje , wakacje ...... Pisał o tym Jakub,że pustki będą ( niestety) do końca sierpnia. Młodzież odpoczywa, tylko My jesteśmy na "warcie" ... ....nieustannie przez cały rok.

Bogdan: Ale za to od września będziemy mieli mnóstwo roboty, bo nowy rok szkolny będzie pierwszym rokiem z obowiązkową matematyką na maturze. Ciekaw jestem, jak będzie za rok wyglądała statystyka pomaturalna, teraz nie zaliczyło matury około 1/5 zdających. Może dzięki temu forum statystyka za bardzo się nie popsuje.

tim : No... Wlasnie duzo osob sie pyta czy juz od mature 2010 jest strona zrobiona. Jakub bedzie mial troche roboty (jezeli nie). Ja bede w III to tez beda kompetencje, troche nerwow i jakos leci. Eta, a ja to co? − tez mlodziez i nie odpoczywam i tez na warcie (nieustannie od kilku miesiecy ). Bogdan, moze.. Zobaczymy.. PS. Soryy za brak polskich znakow alt cos nie dziala.

AS: Skoro się nudzicie,to proponuję takie zadania na rozgrzewkę. 1.Prostokąt o bokach 9 j i 16 j rozciąć na takie dwie części, by można z nich ułożyć kwadrat. 2.Dowieść,że 3! ! ! (3 silnia,silnia,silnia) ma więcej niż 1000 cyfr. 3. Wykazać,że iloczyn 4 liczb całkowitych.różniących się kolejno o 2, powiększony o 16,jest kwadratem zupełnym.

AS: Rozwiązanie zadania 3 podanego przez Mariusza (n) + ( n ) = (n+1) (k) (k+1) (k + 1) Założenie: n,k ∊ N , n ≥ k + 1 (n) + ( n ) = n! n! (k) (k+1) − −−−−−− + −−−−−−−−−−−− = k!*(n−k)! (k+1)!*(n−k−1)! n!*(k+1) n!*(n−k) n!*(k+1) n!*(n−k) = −−−−−−−−−−− + −−−−−−−−−− = −−−−−−−−− + −−−−−−−−−−− k!*(k+1)*(n−k)! (k+1)!*(n−k)! (k+1)!*(n−k)! (k+1)!*(n−k)! n!*(n+1) (n+1)! (n+1) = −−−−−−−−−− = −−−−−−−−−−−−−−− = (k+1)!*(n−k)! (k+1)!*[(n+1)−(k+1)]! (k+1)

Bogdan: Dobry wieczór. Jakoś nikt Asie, nie bierze się za Twoje zadanka, a szkoda, bo są niezłym treningiem umysłowym. Jeśli nikt ich dzisiaj nie ruszy, to spróbuję je rozwiązać, bo warto pokazać rozwiązania takich niestandardowych zadań. Uściślenia wymaga zadanie 2. Zapis 3 ! ! ! oznacza silnię wielokrotną i jej wartość wyraża się liczbą jednocyfrową. Sądząc po poleceniu, chodzi tu o liczbę ((3!)!)! = (6!)! = 720!

AS: Zgadza się, Wpisując 3 wykrzykniki obok siebie wchodziła mi małpka.

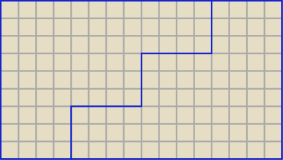
Bogdan: Zadania Asa. Ad. 1. Sposób rozcięcia prostokąta pokazuje rysunek. 9*16 = 12²

tim : Sam próbowałem to rozwiązać i nawet czytałem w książce kilka dni temu ("Histerie matematyczne") o metodzie "schodkowej" i wyleciało mi teraz z głowy...

Bogdan: Ad. zad. 2. Dowieść,że ((3!)!)! ma więcej niż 1000 cyfr. ((3!)!)! = (6!)! = 720! = 1*2*3* ... *99*100*101*...*199*200*201*...*299*300*301*... ...*399*400*401*...*499*500*501*...*599*600*601*...*699*700*701*...719*720 > > (100*101*...*199)*(200*201*...*299)*(300*301*...*399)*(400*401*...*499)*(500*501*... ...*599)*(600*601*...*699) W każdej parze nawiasów znajduje się iloczyn 100 liczb, wstawmy w miejsce każdej liczby liczbę 100 i otrzymujemy oczywistą nierówność: (100*101*...*199)*(200*201*...*299)*(300*301*...*399)*(400*401*...*499)*(500*501*... ...*599)*(600*601*...*699) > (100*100*...*100)*(100*100*...*100)*(100*100*...*100)* *(100*100*...*100)*(100*100*...*100)*(100*100*...*100) = 100⁶⁰⁰ = (10²)⁶⁰⁰ = = 10¹²⁰⁰ Pierwszą cyfrą tej liczby jest 1, za nią jest 1200 zer, a więc ta liczba ma ponad 1000 cyfr, a skoro ((3!)!)! > 10¹²⁰⁰, to liczba ((3!)!)! też ma ponad (i to dużo ponad) cyfr.

Bogdan: Ad. zad. 3. Wykazać,że iloczyn 4 liczb całkowitych różniących się kolejno o 2, powiększony o 16, jest kwadratem zupełnym. Oznaczmy: c − 3, c − 1, c +1, c + 3 to 4 kolejne liczby całkowite. (c − 3) * (c − 1) * (c +1) * (c + 3) + 16 = (x² − 9)(x² − 1) + 16 = x⁴ − 10x² + 9 + 16 = = x⁴ − 10x² + 25 = (x² − 5)², co należało wykazać.

AS: Bogdanie! Nie rozumiem skąd x w równaniu i co ono oznacza. Podaję moją wersję rozwiązania. W = n*(n + 2)*(n + 4)*(n + 6) + 16 = [n*(n + 6)]*[(n + 2)*(n + 4)] + 16 = (n² + 6*n)*(n² + 6*n + 8) + 16 = (n² + 6*n)² + 8*(n² + 6*n) + 4² = (n² + 6*n + 4)² c.n.d.

Squall: Bogdan po prostu pomylił literki. Powinno być "c" zamiast "x" albo odwrotnie

Bogdan: Tak, ma być c, przerwałem pisanie na chwilę, po powrocie do zadania z nawyku wpisałem x, ale mam nadzieję, że idea rozwiązania została zrozumiana. Dziękuję za zauważenie i poprawiam. (c − 3) * (c − 1) * (c +1) * (c + 3) + 16 = (c² − 9)(c² − 1) + 16 = c⁴ − 10c² + 9 + 16 = = c⁴ − 10c² + 25 = (c² − 5)², co należało wykazać.

AS: Bogdanie! Ale z Ciebie niezwykła bomba matematyczna. Gratulacje!

Bogdan: Dziękuję Asie. Też jesteś bardzo dobry i dlatego myślę, że dobrze wiedziałeś, co oznacza literka x w ostatnim zadaniu niefortunnie przez mnie wstawiona w miejsce zastosowanej literki c. Pozdrawiam.

AS: Spośród trójkątów o wierzchołkach: A( m −2 , m −2) , B( m +2, − 4) , C( 3, − m) wybierz ten ,który ma kąt prosty przy wierzchołku C i pole równe 6[j2]. Dla wybranego trójkąta napisz równania prostych w których zawierają się jego boki . mAC = (2*m − 2)/(m − 5) mBC = (−4 + m)/(m − 1) Warunek prostopadłości: mAC*mBC + 1 = 0 2*(m − 1) m − 4 −−−−−−−* −−−−−− + 1 = 0 | *(m − 5)*(m − 1) m − 5 m − 1 2*(m − 1)*(m − 4) + (m − 5)*(m − 1) = 0 (m − 1)*(2*m − 8 + m − 5) = 0 (m − 1)*(3*m − 13) = 0 m − 1 = 0 lub 3*m − 13 = 0 m = 1 lub m = 13/3 Dla m = 1 wierzchołki trójkąta: A(−1,−1) , B(3,−4) , C(3,−1) , jego pole wynosi 6 j² Jest to trójkąt prostokątny o przyprostokątnych równoległych do osi układu wsp. Dla m = 13/3 wierzchołki trójkąta: A(7/3,7/3) , B(19/3,−4) , C(3.−13/3) Równania boków pierwszego trójkąta y = −1 , x = 3 , y = −3*x/4 − 7/4

Eta: Witam AS . Co z drugim "m" ? Można też rozwiązać to zad.podobnie: → → CA o CB = 0 −−−−− iloczyn skalarny wektorów prostopadłych → → i P_Δ=¹₂I d( CA, CB) I = 6 → → CA=[m −5 , 2(m−1)] , CB=[ m −1 , m −4 ] PS: przy tym sposobie rozwiązanie na "m" jest jednoznaczne: m= 1

AS: Drugie uważałem za tak trywialne,że szkoda mi było na to czasu.

Max: Rozwiązuję zad1) z 6 lip 22:34 Dane są: x= (10)^{1_{1 −logz}} y=(10)^{1_{1 −logx}} Wykazać,że z= (10)^{1_{1 − logy}} założenia; x>0 ⊂ 1 −logx≠0 , z>0 ⊂ 1 −logz≠0 y>0 ⊂ 1 −logy≠0 x⊂R₊ \{10} ⊂ y⊂R₊\{10} ⊂ z⊂R₊\{10}

	1		1
logx =		∊ logy=
	1 −logz		1−logx

	logy −1
logx=		∊ y≠1
	logy

1		logy −1
	=
1 −logz		logy

	logy
1−logz=
	logy −1

	logy
logz= 1−
	logy −1

	1
logz=
	1 −logy

z = (10)^{1_{1 − logy}} c.n.d