g.analityczna d4mian: Prosta k jest styczna do okręgu x²+y²−2x−2y−8=0 w punkcie P=(2,4) a) oblicz pole i obwód trójkąta ograniczonego prostą k i osiami układu współrzędnych b) napisz równanie okręgu symetrycznego do danego okręgu względem prostej k

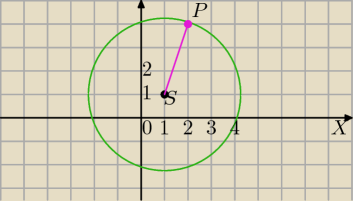
Mila: Prosta k jest styczna do okręgu x²+y²−2x−2y−8=0 w punkcie P=(2,4) (x−1)²−1+(y−1)²−1−8=0 (x−1)²+(y−1)2=10 r=√10 S=(1;1) Sprawdzenie, czy P(2;4) należy do okręgu (2−1)²+(4−1)²=1+9=10 tak Równanie stycznej: s: y=ax+b i s⊥SP, odległość punktu S od prostej wynosi r=√10 s: 4=2a+b⇔b=4−2a s: y=ax+4−2a Teraz spróbuj dalej sam

d4mian: Co dalej z tym fantem zrobić?

Mila: A masz jakiś pomysł? Po słowach:"Równanie stycznej:" podałam własności z których możesz skorzystać.