Zadania maturalne Bogdan: Zadania dla Kuby, zestaw 6.

	sin23x		cos23x
1. Rozwiąż równanie:		−		= 4
	sin2x		cos2x

2. W równaniu 5x² − kx + 1 = 0 dobrać k w ten sposób, aby różnica pierwiastków wynosiła 1.

	1		1
3. Rozwiązać nierówność:		>
	2x − 1		1 − 2x − 1

4. Ze środka kuli wpisanej w stożek widać tworzącą stożka pod kątem α. Znaleźć stosunek objętości kuli do objętości stożka. 5. Iloczyn pewnych trzech liczb pierwszych równa się ich pięciokrotnej sumie. Co to za liczby?

tim : Ja też sobie przy okazji porozwiązuje: 2. ROZWIĄZANE.

Kuba: Dzień dobry, Tim z tego co gdzies tu czytałem wiem, że jesteś w wieku gimnazjalnym, i radzisz sobie z tego typu zadaniami? Ja zaraz zaczne rozwiazywac

tim : Witaj Kubo Więc tak: dobrze się doczytałeś że chodziłem do II GIM / idę do III GIM i czasami radzę sobie z różnymi trudnymi zadaniami . Drugie jest dosyć proste, a w pozostałych życzę Ci powodzenia.

Kuba: Zadanie 2. W równaniu 5x² − kx + 1 = 0 dobrać k w ten sposób, aby różnica pierwiastków wynosiła 1. Δ = k² − 20 > 0 √Δ = √k² − 20 |a| = 5 Wzory skróconego mnożenia i Viete'a a ≠ 0 |x₁ − x₂| = √x₁² + x₂² − 2 * x₁ * x₂ = √(x₁ + x₂)² − 4 * x₁ * x₂ =

	b2		4c		√Δ
= √		−		=
	a2		a		|a|

	√k2 − 20
1 =		/ *5
	5

5 = √k² − 20 podnosze do kwadratu 25 = k² − 20 k² = 45 k = √45 hmhmhmmhmhm dobrze czy nie?

tim : Dobrze. Zrobiłem trochę inaczej (bez wzorów Viete'a) ale wyszło to samo. Możesz wykonać sprawdzenie, ale jest ok.

.: tim ja Ty to zrobiles bez wzorkow

Kuba: Zadanie 5. Iloczyn pewnych trzech liczb pierwszych równa się ich pięciokrotnej sumie. Co to za liczby? x * y * z = 5(x + y + z) W rozkładzie na czynniki tych 3 liczb pierwszych występuje liczba 5 dlatego też 1 liczba z: x, y, z musi być równa 5. zakładam że x = 5 5 * y * z = 5 * (5 + y + z) / :5 y * z = 5 + y + z / −y y * z − y = 5 + z y * (z − 1) = z + 5 y * (z − 1) = (z − 1) + 6 / + 1 − z y * (z − 1) + 1 − z = 6 (z − 1) * (y − 1) = 6 z − 1 = 2 ⇒ z = 3 y − 1 = 3 ⇒ y = 4 4 nie jest liczbą pierwsza z − 1 = 1 ⇒ z = 2 y − 1 = 6 ⇒ y = 7 Odp: Szukane 3 liczby pierwsze to 2, 5, 7.

tim : do pana [.] to było pytanie?

Kuba: tim? "." zadał Ci pytanie jak zorbiłeś zadanie 2 bez wzorków

.: Kubuś juz nie bede sie lepiej wtrącac bo widze ze przeszkadzam tu niektorym

Kuba: Zadanie 3. Nie wiem czy tak można to rozwiązać ale napisze...

1		1		1
	>		/ :
2x − 20		20 − 2x−1		20 − 2x−1

	1		20 − 2x−1		20 − 2x−1
⇒		*		> 0 ⇒		> 0
	2x − 20		1		2x − 20

	− x + 1
⇒		> 0 ⇒ (− x + 1)(x) > 0 ⇒ −x2 + x > 0
	x

Funkcja kwadratowa skierowana wdół + + + −−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−−> − − − 0 1 − − − Ta nierówność przyjmuje wartości dodatnie dla x ∊ (0, 1)

Kuba: oo widze że popełniłem chyba błąd bo w drugiej linijce za znakiem większości powinna być 1(bądź 2⁰) ale już w 3 jest wszystko ok.

Kuba: Zadanie 4. H − czerwone czyli stożka r − niebieskie czyli promień podstawy stożka R − zielone czyli promień kuli No i dalej nie mam bladego pojęcia

tim : Δ = k² − 20 > 0 √Δ = √k² − 20 zał. k² − 20 ≥ 0 k² ≥ 20 k ∊ (−∞,−√20> U <√20, +∞) Podstawiamy do wzorów na x₁ oraz x₂

	k − √k2 − 20
x1 =
	10

	k + √k2 − 20
x2 =
	10

Wiemy, że √k² − 20≥0, więc x₂ > x₁ niezależnie od k. x₂ − x₁ = 1

k + √k2 − 20		k − √k2 − 20
	−		= 1 /*10
10		10

k + √k² − 20 − k + √k² − 20 = 10 2√k² − 20 = 10 /:2 √k² − 20 = 5 /², ale skoro k² − 20 ≥ 0, więc: k² − 20 = 25 k² = 45 k = √45 v k = −√45 Teraz dopiero ze moga byc dwie mozliwosci (chyba ze sie myle)

Kuba: mi się wydaje że nie może być tego drugiego k, ale zobaczymy co na to Bogdan

tim : A dlaczego Kubo. Wykonaj sprawdzenie podstawiając za k = −√45.

Bogdan: Dobry wieczór. Ad. zad. 2. Należało w Twoim rozwiązaniu Kubo rozwinąć założenie: Δ > 0. Wyjaśnij, co ma znaczyć |a| = 5. Jeśli k² = 45, to k² − 45 = 0 ⇒ (k − √45)(k + √45) = 0 Stąd k = √45 = 3√5 lub k = −√45 = −3√5 Są więc dwa rozwiązania. Przedstawię jeszcze jeden sposób rozwiązania (podobny do sposobu Kuby, ale bez potrzeby pierwiastkowania). 5x2 − kx + 1 = 0, Założenie: Δ > 0 ⇒ k² − 20 > 0 ⇒ (k − 2√5)(k + 2√5) > 0 ⇒ k < −2√5 ⋁ k > 2√5

	k		1
x1 + x2 =		, x1x2 =		, (x1 − x2)2 = (x2 − x1)2 = 1
	5		5

(x₁ − x₂)² = x₁² + x₂² + 2x₁x₂ − 4x₁x₂ ⇒ 1² = (x₁ + x₂)² − 4x₁x₂ ⇒

	k2		4
⇒ 1 =		−		⇒ k2 − 45 = 0 ⇒ (k − √45)(k + √45) = 0 ⇒
	25		5

⇒ k = √45 = 3√5 > 2√5 lub k = −√45 = −3√5 < −2√5 Odp.: k = 3√5 lub k = −3√5

Bogdan: Ad. zad. 5. Zaliczone. Od miejsca: y * (z − 1) = z + 5 można było pociągnąć np. tak:

	z + 5		6 + z − 1		6
y =		⇒ y =		⇒ y =		+ 1 i z ≠ 1
	z − 1		z − 1		z − 1

Liczba z−1 jest dzielnikiem naturalnym liczby 6, może więc przyjmować następujące wartości: z − 1 = 1 ⇒ z = 2 i y = 7, z − 1 = 2 ⇒ z = 3 i y = 4, liczba 4 nie jest pierwsza, z − 1 = 3 ⇒ z = 4, liczba 4 nie jest pierwsza, z − 1 = 6 ⇒ z = 7. Odp.: Liczby pierwsze spełniające warunki zadania, to 2, 5, 7. Kubo, jeszcze sugeruję, żebyś w zapisach matematycznych stosował język matematyki używając dostępnych symboli, np.: ⇒, ⇔, ⋁ i innych.

Bogdan: Ad. zad. 3. Nie zaliczone. Spróbuj Kubo jeszcze raz. Pamiętaj o założeniach. Od założeń trzeba rozpoczynać pisanie rozwiązania, nie tylko tego zadania.

Kuba: czyli 2 pierwiastki no nie wiem dlaczego ich w moim rozwiązaniu nie widziałem trudno teraz będę wiedzieć Będę się starał z tymi oznaczeniami, ale chyba nie one tu najważniejsze tylko matura 25 sierpnia. Sam nie wiem skąd |a| miałobyć tylko a = 5 a jak zadanie 3? a co do zadania 1 to doszedłem (na kartce oczywiście) do sin²α = ³₄ ale jakieś bzdury mi wychodzą. Moge prosić o rozwiązanie tych 2 zadań tzn. 1 i 4?

Bogdan: Stosowanie właściwej terminologii w każdej dziedzinie jest bardzo istotne, jej znajomość świadczy o posiadanych kompetencjach. Jeśli zależy Ci na jak najlepszym odbiorze Twojej pracy, to wykaż, że dojrzale podchodzisz do egzaminu, że posiadasz właściwe kompetencje i zasługujesz na zaliczenie matury (kiedyś mówiło się − świadectwa dojrzałości). Stosuj w zapisach matematycznych właściwą dla tej dziedziny symbolikę. Poczekam jednak na Twoje rozwiązania zadań 1, 3 i 4. W zadaniu 4 wprowadź na rysunku kąt α, oznacz również inne kąty, w ich oznaczeniach ma występować α. W zadaniu 1 i 3 zacznij od założeń.

Kuba: ale przecież 3 jest do góry^^^^^^ źle?

Kuba: ale przecież 3 jest do góry^^^^^^ źle?

Bogdan: Przecież napisałem, że zadanie 3 nie jest zaliczone.

Kuba: ahhh no tak

Kuba: Moim zdaniem pisanie zadania (tu jest czasochłonne ale badziej utkwi mi w pamięci) ale pisanie jeszcze raz najprawdopodobniej znów błędnie, to wielki błąd bo co, będe zapamiętywał złe rozwiązania tego typu zadań? Dlatego pisze zadania 1, 3 i 4 nie zrobie bo nie potrafie, kto potrafi niech napisz

Bogdan: Rozpocznę w takim razie rozwiązania, a Ty spróbuj je dokończyć. Ad. zad. 1. Założenia: sin²x ≠ 0 i cos²x ≠ 0

sin2x		cos23x
	−		= 4 / * sin2xcos2x ⇒
sin2x		cos2x

⇒ sin²3xcos²x − sin²xcos²3x = 4sin²xcos²x ⇒ ⇒ (sin3xcosx + sinxcos3x)(sin3xcosx − sinxcos3x) = (2sinxcosx)² Przypomnij sobie wzory: sin(α + β), sin(α − β), sin2α

tim : Bogdanie, a moje może być ?

Bogdan: Ad. zad. 3.

1		1
	>
2x − 1		1 − 2x−1

Założenia: 2^x ≠ 2⁰ ⇒ x ≠ 0 i 2^x−1 ≠ 2⁰ ⇒ x ≠ 1

	1
Dla ułatwienia obliczeń podstawiamy: 2x = t i t > 0, 2x−1 =		t
	2

1		1		1		−2		1		2
	>		⇒		>		⇒		+		> 0
t − 1		1   1 − t   2		t − 1		t − 2		t − 1		t − 2

Teraz Twoja kolej, Kubo.

Bogdan: Tiumie, Twoje rozwiązanie jest poprawne, nie mam do niego uwag

Bogdan: Przepraszam Tim, miało być Timie

Bogdan: Tim, spróbuj rozwiązać zadanie 4 ze stożkiem.

Kuba:

1		2
	+		> 0 / * (t − 1)(t − 2)
t − 1		t − 2

(t − 2) + 2(t − 1) > 0 t − 2 + 2t − 2 > 0 3t > 4 / :3 t > ³₄ 2^x > ³₄

Bogdan: Kuba, źle, nie wolno mnożyć nierówności przez wyrażenie zawierające zmienną, jeśli nie znamy znaku tego wyrażenia.

Bogdan: Należy sprowadzić najpierw lewą stronę do wspólnego mianownika i potem zapisać nierówność w postaci równoważnej nierówności wielomianowej.

Kuba: :(

Kuba: czyli że jak

1 − 1
t − 1 −1

tak to sprowadzić do wspólnego mianownika?

Bogdan:

1		2		t − 2 + t − 1
	+		> 0 ⇒		> 0 ⇒
t − 1		t − 2		(t − 1)(t − 2)

	2t − 3		3
⇒		> 0 ⇔ 2(t −		)(t − 1)(t − 2) > 0
	(t − 1)(t − 2)		2

Spróbuj kontynuować.

Eta: Witam Bogdanie! Hmm.... widzę błąd...

	t−2 +2t −2
		>0
	(t−1)(t−2)

Bogdan: Oczywiście Eto, witaj , też zauważyłem i już pisałem poprawkę, zobaczyłem sposób sprowadzania do wspólnego mianownika przez Kubę i z rozpędu nie uwzględniłem dwójki w liczniku. Basia wróciła.

t − 2 + 2t − 2		3t − 4
	> 0 ⇒		> 0 ⇔
(t − 1)(t − 2)		(t − 1)(t − 2)

	4
⇔ 3(t −		)(t − 1)(t − 2) > 0
	3

Kuba: przepraszam za jakies jeszcze 30 min bede mógł to na spokojnie przeanalizować, a póżniej kontynuować.

Eta: Ok

Bogdan: + + + + + + −−−−−−−−−−−(1)−−−−−−−−−−(⁴₃)−−−−−−−−−−(2)−−−−−−−−−−−>t − − − − − − 1 < t < ⁴₃ lub t > 2

	4		4
2y =		⇒ y = log2		⇒ y = log24 − log23 = 2 − log23
	3		3

2⁰ < 2^x < 2^{2 − log₂3} lub 2^x > 2¹ Na podstawie monotoniczności funkcji logarytmicznej otrzymujemy: 0 < x < 2 − log₂3 lub x > 1, założenia są spełnione.

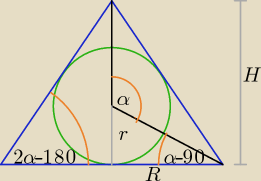
Bogdan: Zadanie 3 jest rozwiązane, przechodzimy do zadania 4. Objętość kuli V_k = U{4}[3}πr³

	1
Objętość stożka Vs =		πR2H
	3

	Vk		4   πr3 3		4r2 * r
Mamy obliczyć k =		=		=
	Vs		1   πR2H 3		R2 * H

	r		r
k = 4 * (		)2 *
	R		H

Wyznacz Kubo odpowiednie funkcje trygonometryczne kąta α.

Bogdan:

	4
Objętość kuli jeszcze raz: Vk =		πr3
	3

Kuba: już zaczynam.

Kuba: Dobrze, bo nie chce znów pisać błędnie? [sin(3x + x)][sin(3x − x)] = sin²4x

Eta: Kubo ....... 2sinxcosx= sin2x to : ( 2sinxcosx)² = sin²2x

Bogdan: Lewa strona dobrze, prawa nie, nawiasy kwadratowe są zbędne. (2sinxcosx)² = sin²2x Masz więc: sin4x*sin2x = sin²2x Rozwiąż to równanie.

Kuba: ja dziś całkowicie nie myśle, a jak myśle to błędnie, przeprasza. może dziś jak się prześpie, będzie lepiej. sin8x = sin²2x

Bogdan: Życzę wszystkim dobrej nocy

Kuba: Wzajemnie Dobranoc

Bogdan: To jeszcze podpowiedź. sin4x*sin2x = sin²2x ⇒ sin4x*sin2x − sin²2x = 0 ⇒ sin2x(sin4x − sin2x) = 0 sin2x = 0 lub sin4x = sin2x W dzień Kubo dokończysz, dobranoc.

Kuba: Bogdanie możesz dokońca zrobić Zadanie 1.(musze się dobrze funkcji trygonometrycznej nauczyć)

Kuba: Dziś zabardzo czasu nie mam, ale mam prośbe Bogdanie wrzucisz kolejne 5 zadań? i te zadanie 1 i 4 pokażesz szczegółowo jak rozwiązać?

Kuba: jutro koło 11 już powinienem być w domu to zabiore się odrazu za to, już napewno.

Bogdan: Dzień dobry. Ad. zad. 1, pełne rozwiązanie.

sin23x		cos23x
	−		= 4
sin2x		cos2x

Założenia: 1. sin²x ≠ 0 ⇒ x ≠ k*π, k ∊ ℂ

	π
2. cos2x ≠ 0 ⇒ x ≠		+ k*π
	2

	1
Z założeń 1 i 2 otrzymujemy: x ≠ k*		π
	2

Po obustronnym wymnożeniu równania przez sin²x cos²x mamy: sin²3xcos²x − sin²xcos²3x = 4sin²xcos²x ⇒ ⇒ (sin3xcosx + sinxcos3x)(sin3xcosx − sinxcos3x) = (2sinxcosx)² ⇒ ⇒ sin(3x + x) * sin(3x − x) = (sin2x)² sin4x*sin2x = sin²2x ⇒ sin4x*sin2x − sin²2x = 0 ⇒ sin2x(sin4x − sin2x) = 0 sin2x = 0 lub sin4x = sin2x

	1
2x = k*π ⇒ x = k*		π, sprzeczne z założeniem
	2

lub 4x = 2x + k*2π ⇒ 2x = k*2π ⇒ x = k*π, sprzeczne z założeniem,

	1		1
lub 4x = π − 2x + k*2π ⇒ 6x = π + k*2π ⇒ lub x =		π + k*		π
	6		3

Z ostatniego rozwiązania musimy usunąć punkty sprzeczne z założeniem, najwygodniej jest narysować oś (na rysunku litera p oznacza π) i zaznaczyć na niej punkty sprzeczne z założeniem (na rysunku puste kółeczka) oraz zaznaczyć punkty opisane zależnością

	1		1
x =		π + k*		π (na rysunku pełne czerwone kółeczka), nie zaznaczamy przy
	6		3

tym punktów spełniających uzyskaną zależność, ale sprzecznych z założeniem.

	1
Odp.: x = ±		π + k*π
	6

Bogdan: Ad. zad. 4. r − długość promienia kuli wpisanej w stożek, R − długość promienia podstawy stożka, H − długość wysokości stożka. a − miara kąta, pod którym widać tworzącą stożka ze środka kuli (grecka literka α nie chciała się wpisać na rysunek).

r
	= tg(a − 90o) = −tg(90o − a) = −ctga ⇒ r = −Rctga.
R

H
	= tg(2a − 180o) = −tg(180o − a) = tg2a ⇒ H = Rtg2a
R

	4		1
Objętość kuli: Vk =		πr3, objętość stożka: Vs =		πR2H
	3		3

	Vk		4   πr3 3		4r3		4*(−Rctga)3
k =		=		=		=		=
	Vs		1   πR2H 3		R2H		R2*Rtg2a

	−4R3ctg3a
=		= −4*ctg3a*ctg2a
	R3tg2a

nick: