Zadania dla Kuby, zestaw 5. Bogdan: Zadania dla Kuby, zestaw 5. 1. Wyznacz te wartości rzeczywiste parametru k, dla których okrąg opisany równaniem: x² + y² + 2x − 6y + 2k − 2 = 0 jest styczny do prostej o równaniu 4x + 3y + 5 = 0. 2. Znajdź funkcję liniową, która spełnia dla każdego x ∊ ℛ, następujące warunki: f(−3x) = −3f(x) + 12 f(x − 1) = 5 + f(x) 3. Dany jest okrąg o promieniu R. Na okręgu tym opisujemy wielokąty foremne. Długości boków tych wielokątów tworzą pewien ciąg. a) Wyznacz wzór na wyraz ogólny tego ciągu. b) Uzasadnij, że badany ciąg jest malejący.

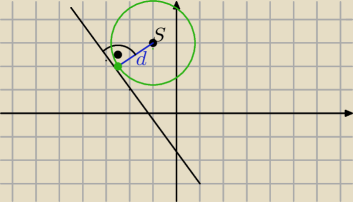
Kuba: Zadanie1. 4x + 3y + 5 = 0 / −4x − 5 3y= − 4x − 5 /:3

	4		5
y = −		x −
	3		3

x² + y² + 2x − 6y + 2k − 2 = 0 x² + y² − 2ax − 2by + c = 0 środek okręgu S = (a, b) a = −1 b = 3 d na niebiesko

	|−4 + 9 + 5|		10
d =		=		= 2
	√42 + 32		5

d = r 4 = 16 + 9 − 2k + 2 4 = 27 − 2k /+2k − 4 2k = 23 k = 11,5 Nie wiem czy to jest do końca dobrze...

Kuba: Zadanie 2 Funkcja liniowa ma wzór f(x) = ax + b f(−3x) = −3f(x) + 12 f(x − 1) = 5 + f(x) f(−3x) = −3ax + b f(x − 1)=a(x − 1) + b= ax − a + b −3ax + b = −3ax −3b + 12 / + 3ax ax − a + b = 5 + ax + b / − ax b= −3b + 12 / + 3b −a + b = 5 + b / − b b = 3 a = −5 Odp: Funkcja liniowa której szukałem ma wzór f(x) = −5x + 3

Kuba: a do tego 3 nie mam pomysłu

Bogdan: Ad. zadanie 1. Trzeba poprawić i dokończyć. Wyznacz długość r promienia okręgu, przypominam, jeśli okrąg dany jest równaniem:

	a		b
x2 + y2 + ax + by + c = o, to środek okręgu S = (xo, yo), xo = −		, yo = −		,
	2		2

długość promienia tego okręgu r = √x_o² + y_o² − c , następnie porównaj wyznaczone r z wyznaczoną wcześniej odleglością d, stąd otrzymasz k. Ad. zadanie 2. Jest ok. Drobna uwaga, cytuję Twój zapis: −3ax + b = −3ax −3b + 12 / + 3ax Na poziomie liceum w zasadzie nie stosuje się zapisu za równaniem: / + 3ax, można go stosować w przypadku mnożenia, dzielenia, podnoszenia do potęgi obu stron równania, natomiast dodawania lub odejmowania nie sygnalizujemy w ten sposób, nie jest to jednak oczywiście nic złego, powiedziałbym raczej − nie wypada. Jeszcze raz Twój zapis: −3ax + b = −3ax −3b + 12 / + 3ax ax − a + b = 5 + ax + b / − ax Powinno być: −3ax + b = −3ax −3b + 12 ⇒ 4b = 12 ⇒ b = 3 ax − a + b = 5 + ax + b ⇒ b = 5 Ad. zadanie 3. Spróbuj jeszcze raz.

Kuba: Każdy uczy inaczej co do tego zapisu dodawania lub odejmowania nas uczono żeby sygnalizować wszystkie takie działania żeby nie było żadnych nie domówień tych zadań już nie będe poprawiać bo szkoda czasu zrozumiałem Twoje uwagi. A 3 nie ciągle nie daje się rozwiązać...

Kuba: Korekta: "A 3 ciągle nie daje się rozwiązać..."

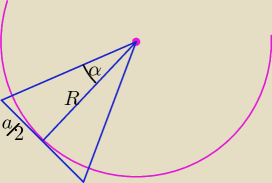
Bogdan: Ad. zad. 3.

	360o		180o
2α =		⇒ α =		,
	n		n

n − liczba boków n−kąta foremnego opisanego na okręgu o promieniu R, a − długość boku n−kąta foremnego, n ∊ ℕ i n ≥ 3. Wyznacz długość a w zależności od R i n.

Bogdan: Zadanie 1 trzeba poprawić i dokończyć.

Kuba: Do zadania 1. do środka okręgu jest dobrze(środek jest już zły) środek okręgu S = (x_o, y_o)

	a
xo = −
	2

	b
yo = −
	2

	1		3
S = (		, −		)
	2		2

	9   |2 − + 5|   2		2,5		2,5		1
d =		=		=		=
	√42 + 32		√25		5		2

r = √x_o² + y_o² − c r = √(¹₂)² + (− ³₂)² − 2k + 2 r = √¹₄ + ⁹₄ − 2k + 2 r = √¹⁰₄ − 2k + 2 r = ¹₂ − 2k

1		1
	=		− 2k
2		2

2k = 0 k = 0 Teraz Bogdanie się zgadza?

Kuba: a zadania 3 naprawde nie potrafie wyonać nawet z tym co podesłałeś Prosze pokaż jak je zrobić.

Bogdan: Ad. zad. 1. Wyznacz te wartości rzeczywiste parametru k, dla których okrąg opisany równaniem: x² + y² + 2x − 6y + 2k − 2 = 0 jest styczny do prostej o równaniu 4x + 3y + 5 = 0. Okrąg: a = 2, b = −6, c = 2k − 2

	2		−6
xo = −		= −1, yo = −		= 3,
	2		2

środek okręgu S = (−1, 3), miałeś w pierwszej wersji dobrze, r = √(−1)² + 3³ − 2k + 2 = √12 − 2k d = 2 i d = r, stąd √12 − 2k = 2 ⇒ 12 − 2k = 4 ⇒ k = 4. Sprawdzenie: jeśli k = 4 to r = √12 − 2k = √12 − 8 = √4 = 2 = d. Odp.: k = 4.

Eta: Kuba..... S( −1, 3) ........ dobrze policzyłeś poprzednio. bo:

	−2		6
xo=		= −1 , yo=		= 3
	2		2

c= 2k − 2 więc: r=√a² +b² −c r= √10 −2k +2 => r=√12−2k więc 12 −2k >0 => k < 6 d= 2 to r= d => √12−2k = 2 12 −2k = 4 => k = 4

Kuba: ehhhh, pisałem że szkoda czasu:( nie wiem po co to liczyłem ...

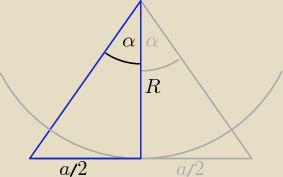
Bogdan: Ad. zad. 3.

	360o		180o
Jeśli na okręgu opisano n−kąt foremny, to miara kąta 2α =		, a stąd α =		.
	n		n

Popatrz na rysunek i mając dane R oraz n wyznacz długość a. Przecież to jest tylko trójkąt prostokątny.

Kuba:

	1   a 2
tgα =
	R

2R * tgα = a

	360o
2 * α =
	n

	360o
α =
	2n

	180o
α =
	2n

a =2R * tg * ^180o_n Przy trójkącie n=3 a_n = 2R * tg * ^180o_n

Kuba: Dobrze jest ?

Bogdan: Używaj znaku ⇒ Zapisy powinny być takie:

	360o		180o
α =		⇒ α =
	n		n

	1   a 2		180o
tgα =		⇒ a = 2Rtgα ⇒ a = 2Rtg
	R		n

Znak * w zapisie tg * ^180o_n wpadł chyba za sprawą chochlika. Każdy ciąg posiada wyraz pierwszy, jaki jest tutaj a₁ ?

Kuba: a₁ = 2R * tg ^180o₃

Bogdan: Dobrze, to teraz podaj wzór na wyraz ogólny ciągu.

Kuba: ahaa a_n = 2R * tg ^180o_n+2

Bogdan: Dobrze. No i co, takie trudne było? Uzasadnij jeszcze, że ciąg jest malejący.

Kuba: hmmmm a_n+1 = 2R * tg ^180o_{n + 3} a_n = 2R*tg ^180o_{n + 2} a_n+1 − a_n = 2R( tg ^180o_{n + 3} − tg ^180o_{n + 2} n ∊ N₊ ^180o_{n + 2} ∊ (0, ^180o ₂) ^180o_{n + 3} ∊ (0, ^180o ₂) ^180o_{n + 2} > ^180o_{n + 3} ^180o_{n + 3} < ^180o_{n + 2} ⇒ ^180o_{n + 3} − ^180o_{n + 2} < 0 czyli a_n+1 − a_n < 0 dany ciąg jest malejący

Kuba: Bogdanie, nie było by problemem dawać większą ilość zadań na dzień? może 10?;>

Bogdan: Jeśli chcesz napisać a_{n + 1}, a nie a_n + 1, to po a, za znakiem podkreślnika zastosuj klamry { } wpisując {n + 1}. Dobrze uzasadniłeś, należało jednak dopisać: funkcja tgx jest funkcją rosnącą, więc

	180o		180o		180o		180o
z		<		wynika, że tg		< tg		⇒
	n + 3		n + 2		n + 3		n + 2

⇒ a_{n + 1} < a_n Dziękuję za owocną współpracę i dobranoc.

Bogdan: Wstawiaj tutaj zadania, z którymi masz problemy. Jak widzisz, rozpatrzenie trzech zadań zajmuje dość dużo czasu, przy 10 byłoby trudno tak dokładnie je omawiać.

Kuba: to ja dziękuje, dobranoc

Kuba: To moze podniesiemy ich liczbe o 2?

Bogdan: Dobrze, przed południem wstawię 5 zadań.