? Patryk: W prostej o równaniu 2x+y−6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+y²−2y−4=0 . Oblicz współrzędne wierzchołków tego kwadratu. podam tylko dwa wierzchołki jakie i wyszły sprawdzicie czy dobrze ? a(1,4) b(3,0) w książce jest zupełnie inaczej

Artur_z_miasta_Neptuna: przecież to są złe punkty ... wstaw do wzoru okręgu ... przecież te punkty nie należą do tego okręgu

Patryk: nie muszą należeć do okręgu

Patryk: opisanego nie wpisanego

Artur_z_miasta_Neptuna: ajjj ... sorki ... pokićkałem opisany kwadrat z wpisanym

Patryk: częsty błąd

Artur_z_miasta_Neptuna: punkt styczności okręgu i tej prostej to

Patryk: P(2:2)

Artur_z_miasta_Neptuna: x² + y²−2y − 4=0 ⇔ x² + (y−2)² −4−4 = 0 ⇔ x² + (y−2)² = 8 stąd r=√8 = 2√2 stąd bok kwadratu to 4√2 <−−− i tu zapewne masz błąd

Artur_z_miasta_Neptuna: kuźwa ... x² + y²−2y − 4=0 ⇔ x² + (y−1)² −1−4 = 0 ⇔ x² + (y−2)² = 5 dzisiaj takie babole robię

Patryk: hej a nie x²+(y−1)²=5 ?

Artur_z_miasta_Neptuna: ostatecznie −−− wygląda dobrze ... a w odpowiedzi niby jakie punkty są

Patryk: już podaje

Patryk: (0,−4) (0,6) (−4,4) (4,−2). one chyba tworzą prostokąt

Patryk: ale błędy w tej książce dają

Artur_z_miasta_Neptuna: no to są to złe odpowiedzi ... w dodatku tworzą olbrzymi kwadrat

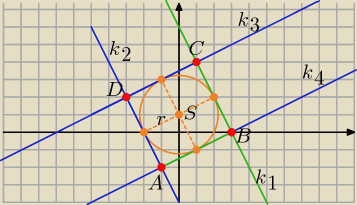
Bogdan: Rysunek do zadania S = (0, 1) − środek okręgu, r = √5 − długość promienia okręgu. k₁: y = −2x + 6

Patryk: dodam ,że to nie jeden błąd który znalazłem w tej ksiązce

Patryk: Bogdan, mam tak samo ,ale dzięki