zadania dla Kuby, zestaw 4.
Bogdan:
zadania dla Kuby, zestaw 4.
Mam nadzieję Kubo, że się nie zniechęciłeś i jesteś gotów na następne wyzwania.
1. Punkty A = (−3, −2), B = (2, 1), C = (4, 5) są wierzchołkami równoległoboku ABCD.
Wyznacz współrzędne wierzchołka D oraz oblicz pole tego równoległoboku.
2. Nie korzystając z tablic ani kalkulatora oblicz: cos105o * cos75o.
3. Dana jest funkcja: f(x) = log9(2x + 1). Rozwiąż nierówność f(f(2x)) ≤ 0.
3 lip 17:23
Kuba: NIe oczywiście że się nie zniechęciłem

ja walcze do końca w tym przypadku do 25 sierpnia

Zaraz zaczne robić któreś z tych zadań.
3 lip 23:25
tEa:
Jak idzie Kuba ?....
4 lip 00:01
Kuba:
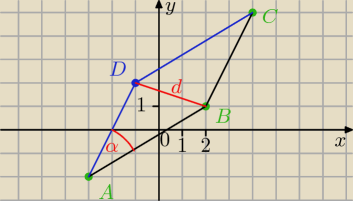
Zadanie 1.
Dane
A = (−3, −2)
B = (2, 1)
C = (4, 5)
są to wierzchołki równoległoboku (zielone) połaczone (czarne)
|AD| = |BC| i |AB| = |DC| <−−−− wlasność równoległoboku
−−> −−>
AB = DC
−−>
AB = [5, 3]
−−>
DC = [4 − x
d, 5 − y
d]
5 = 4 − x
d / −5 + x
d
3 = 5 − y
d /−3 + y
d
x
d = −1
y
d = 2
D = ( −1, 2) mamy D (niebieskie)
Długość |AB|
|AB| =
√(5)2) + (3)2 =
√25+9 =
√34
Długość |BC|
|BC| =
√(2)2) + (4)2 =
√4+16 =
√20 = 2 *
√5
Długość przekątnej d (|DB|)
|DB| =
√(3)2) + (−1)2 =
√9+1 =
√10
Twierdzenie cosinusów
10 = 20 + 34 − 2 *
√34 *
√20 * cosα
10 = 54 − 2 *
√680 *cosα / −10 + 2 *
√680 * cosα
2 *
√680 * cosα = 44 / : 2
√680 * cosα = 22 / :
√680
cosα ≈ 0,844
sin
2 α + cos
2 α = 1
sin
2 α = x
x + 0,712 = 1
x= 0,288
sin
2 α = 0,288
sinα = 0,537
Pole równoległoboku
P ≈
√34 *
√20 * 0,537 ≈ 14 {j
2]
Odp: Współrzędne wierzchołka D to (1, 2), Pole tego równoległoboku wynosi 14 [j
2]
4 lip 00:54
Kuba: powoli ale chyba do przodu

4 lip 00:55
Bogdan:

Wierzchołek D i pole równoległoboku wyznaczyłeś poprawnie. Do sposobu wyznaczenia
wierzchołka D nie mam uwag, natomiast pole wyznaczyłeś w najgorszy możliwy sposób,
tracąc przy tym dużo czasu. Łatwiej i zdecydowanie prościej wyznacza się pole równoległoboku
następująco:
A = (−3, −2), B = (2, 1), C = (4, 5), D = (−1, 2)
→
AB = [5, 3]
→
AD = [2, 4]
| 5 3 |
Pole P = | | | | = |20 − 6| = 14 [j
2]
| 2 4 |
Proste i łatwe, prawda?
4 lip 01:19
tEa:
Pole równoległoboku można prościej policzyć:
korzystając z wyznacznika pary wektorów zaczepionych w jednym punkcie.
np: → → → →
P= Id(CB, CD)I CB= [−2,−4] CD= [−5,−3]
P=I −2*(−3) − (−4)*(−5)I = I6 − 20 I = 14 [j2]
4 lip 01:24
Kuba: Zadanie 2.
wzór redukcyjny tzw "coco sisi".
cos105
o = cos(45
o + 60
o) = cos45
o * cos60
o − sin45
o * sin60
o =
| | √2 | | 1 | | √2 | | √3 | | √2 | | √6 | |
= |
| * |
| − |
| * |
| = |
| − |
| =
|
| | 2 | | 2 | | 2 | | 2 | | 4 | | 4 | |
cos75
o = cos(45
o + 30
o) = cos45
o * cos30
o − sin45
o * sin30
o =
| | √2 | | √3 | | √2 | | 1 | | √6 | | √2 | |
= |
| * |
| − |
| * |
| = |
| − |
| =
|
| | 2 | | 2 | | 2 | | 2 | | 4 | | 4 | |
| | √2 − √6 | | √6 − √2 | |
cos105o * cos75o = |
| * |
| =
|
| | 4 | | 4 | |
| | √12 − √4 − √36 + √12 | | 2√3 − 2 − 6 + 2√3 | |
= |
| = |
| =
|
| | 4 | | 4 | |
| | 4√3 − 8 | | 4(√3 − 2) | |
= |
| = |
| = √3 − 2
|
| | 4 | | 4 | |
cos105
o * cos75
o =
√3 − 2
4 lip 01:28
Kuba: No tak

może zapamiętam Twój sposób.
4 lip 01:29
tEa:
Kuba ?.......
sprawdź ,gdzie popełniłes błąd?
4 lip 01:32
Kuba: Ale np. tego wzoru Bogdanie nie ma w karcie wzorów:(
Możesz mi go przypomnieć? (pamiętam że się mnożyło na krzyż)
4 lip 01:34
Bogdan:
Proszę znaleźć prostsze rozwiązanie zadania 2.
4 lip 01:36
Bogdan:
Wyznacznik 2 stopnia:
|a b|
| | = ad − bc
|c d|
4 lip 01:38
Kuba: aaaa już wiem w ostatnim zadaniu pomnożyłem liczniki ale nie pomnożyłem mianowników.
Dzięki Tea

ale juz tego zmieniac nie będę

4 lip 01:38
Kuba: ale dlaczego przeciez jest dobrze rozwiązane z małym błędem ale już przedyskutowanym.
nie potrafie znaleść prostrzego
jedyne co mi się nasuwa coco − sisi
coco + sisi
ale nie wyobrażam sobie rozwiazanie tego
4 lip 01:41
Bogdan:
Jest wzór w tablicach wzorów na pole trójkąta. Pole równoległoboku obliczymy tym wzorem
| | 1 | |
pomijając w nim czynnik |
| . |
| | 2 | |
4 lip 01:42
Kuba: W moich tablicach(cke sciagnietych tego roku) sa 3 wzory na pole trójkąta
1/2 ah
1/2absinγ
(abc)/(4R)
nic więcej
4 lip 01:45
tEa:
Kuba zmęczył się i poszedł

Dobranoc Wszystkim

4 lip 01:47
Kuba: zmęczony jestem ale spać pójde zaraz

Tea Dobranoc

4 lip 01:48
Bogdan:
Podaję ten wzór na pole trójkąta z tego arkusza:
| | 1 | |
PΔ = |
| |(xB − Xa)(yC − yA) − (yB − yA)(xC − xA)| |
| | 2 | |
4 lip 01:51
Kuba: no tak jest, przepraszam

Dobranoc

4 lip 01:53
Bogdan:
Zapraszam wszystkich do znalezienia najprostszego rozwiązania zadania 2, przypomnę treść:
Nie korzystając z tablic ani kalkulatora oblicz: cos105o * cos75o.
4 lip 01:55
Bogdan:
Dobranoc

4 lip 01:56
Kuba: już wiem

chyba dobrze cos105o * cos75o. to poprostu to samo tylko ze przy 105 będzie minus
ale potem i tak jest dodatni, Tak?
4 lip 02:06
Bogdan:
Kuba, nie oto chodzi.
Proszę przedstawić pełne i najprostsze rozwiązanie zadania 2.
4 lip 02:19
Bogdan:
Chochlik, miało być: "nie o to chodzi"
4 lip 02:20
tEa:
Ja podałabym tak::
cosα +cosβ= 2 cos
α+β2*cos
α −β2
zatem:
cos105
o*cos75
o=
12*cos
180o+30o2*cos
180o−30o2=
| | cos180o +cos30o | | −1 +√32 | |
= |
| = |
| =
|
| | 2 | | 2 | |
4 lip 02:21
tEa:
Bogdanie!
Podaj ten najprostszy sposób

bo nie zasnę

4 lip 02:23
tEa:
Oczy mi sie już kleją

oczywiście bez
12 w drugiej linijce!
4 lip 02:27
Bogdan:
Dobrze, zaraz podam

4 lip 02:28
tEa: 
ok.

4 lip 02:29
tEa:
Myślę,że ten mój sposób jest prostszy niż podany przez Kubę ?
4 lip 02:31
4 lip 02:34
tEa:
Idę

Dobranoc! Miłych snów

4 lip 02:37
Bogdan:
Są 2 proste sposoby, pokazuję jeden z nich, drugi pokażę potem.
cos105
o = sin(90
o − 105
o) = sin(−15
o) = −sin15
o.
cos75
o = sin(90
o − 75
o) = sin15
o.
| | cos2α − 1 | |
Wzór: cos2α = 1 − 2sin2α ⇒ −sin2α = |
| |
| | 2 | |
| | cos30o − 1 | | | | √3 − 2 | |
cos105o * cos75o = −sin215o = |
| = |
| = |
| |
| | 2 | | 2 | | 4 | |
4 lip 02:39
Bogdan:
No właśnie Eto, podałaś drugi prosty sposób

4 lip 02:41
tEa:

Idę zatem spokojnie spać

Dobranoc!
4 lip 02:54
Kuba: no Bogdanie, to dobrze myślałem, tylko już potem w nocy
wyłańczało mi się myślenie

po przekształceniu są to
te same funkcje tylko przy tej gdzie jest 105
o będzie minus.
Można nawet sprawdzić na kalkulatorze, że cos105
o to
Liczba −0,288, a cos 75
o to liczba +0,288. wydaje mi się
Więc że się nie myliłem Bogdanie

tylko do końca tego nie
Przemyślałem

4 lip 11:42
Kuba: wyłączało

xD
4 lip 11:47
Kuba: 3 nie potrafie:(
4 lip 12:03
Bogdan:
Dzień dobry.
Zadanie 3 czeka na rozwiązanie. Przypomnę treść.
Dana jest funkcja: f(x) = log9(2x + 1). Rozwiąż nierówność f(f(2x)) ≤ 0.
Zapraszam każdego do jego rozwiązania.
W przypadku, gdy nikt nie pokaże rozwiązania, zamieszczę je późnym wieczorem.
Kubo, zadanie 2 w wersji, którą przedstawiłeś, zostałoby na maturze zaliczone, błąd rachunkowy
nie miał wpływu na sposób rozumowania. Za chwilę zamieszczę kolejne 3 zadania i wyłączę się,
będę tu wieczorem.
4 lip 12:40
Kuba: Zadanie 3.
f(x) = log9(2x + 1)
Już chyba wiem Dziedziną jest:
2x + 1 > 0
x > − 12
f(2x) = log9(4x + 1)
4x + 1 > 0
x > − 14
f(f(2x)) = log9(2(log9(4x + 1)) + 1)
2(log9(4x + 1)) + 1 > 0 /− 1 a potem :2
log9(4x + 1) > −12
log9(4x + 1) > log9 13 / : log9
4x + 1 > 13
4x > − 23 : 4
x > − 16
log9(2(log9(4x + 1)) + 1) ≤ 0
log9(2(log9(4x + 1)) + 1) ≤ log9 1 /log9
2(log9(4x + 1)) + 1 ≤ 1 / −1
2(log9(4x + 1)) ≤ 0 /:2
log9(4x + 1) ≤ 0
log9(4x + 1) ≤ log9 1 /:log9
4x + 1 ≤ 1
4x ≤ 0
x ≤ 0
cześć wspólna pierwszych 3 to (−16, + ∞)
Wynik końcowy
x∊ (−16, 0 >
4 lip 17:36
Kuba: Mam nadzieje, że dobrze to jest rozwiązane

4 lip 17:38
Bogdan:
Dobry wieczór.
Nareszcie prawdziwie lipcowy, upalny dzień, ani kropli deszczu.
Kubo, nie mów więcej: nie potrafię, nie umiem, nie wiem. Jeśli zadanie nie chce Ci się
poddać, chociaż wolę inne określenie, jeśli zadanie w Twoim odczuciu nie chce Ci się oddać,
to znaczy, że źle się za nie zabrałeś. Odczekaj i spróbuj z innej strony, tak, jak postąpileś
z zadaniem nr 3. Poza drobnymi niuansami, o których nie warto nawet mówić, nie można
się przyczepić do Twojego rozwiązania. Zaliczone

4 lip 21:20
Kuba: Dobry wieczór

to świetnie

No tak dziś jest super upalnie aż do teraz

4 lip 21:35
 ja walcze do końca w tym przypadku do 25 sierpnia
ja walcze do końca w tym przypadku do 25 sierpnia Zaraz zaczne robić któreś z tych zadań.
Zaraz zaczne robić któreś z tych zadań.
 Zadanie 1.
Dane
A = (−3, −2)
B = (2, 1)
C = (4, 5)
są to wierzchołki równoległoboku (zielone) połaczone (czarne)
|AD| = |BC| i |AB| = |DC| <−−−− wlasność równoległoboku
−−> −−>
AB = DC
−−>
AB = [5, 3]
−−>
DC = [4 − xd, 5 − yd]
5 = 4 − xd / −5 + xd
3 = 5 − yd /−3 + yd
xd = −1
yd = 2
D = ( −1, 2) mamy D (niebieskie)
Długość |AB|
|AB| = √(5)2) + (3)2 = √25+9 = √34
Długość |BC|
|BC| = √(2)2) + (4)2 = √4+16 = √20 = 2 * √5
Długość przekątnej d (|DB|)
|DB| = √(3)2) + (−1)2 = √9+1 = √10
Twierdzenie cosinusów
10 = 20 + 34 − 2 * √34 * √20 * cosα
10 = 54 − 2 * √680 *cosα / −10 + 2 * √680 * cosα
2 * √680 * cosα = 44 / : 2
√680 * cosα = 22 / : √680
Zadanie 1.
Dane
A = (−3, −2)
B = (2, 1)
C = (4, 5)
są to wierzchołki równoległoboku (zielone) połaczone (czarne)
|AD| = |BC| i |AB| = |DC| <−−−− wlasność równoległoboku
−−> −−>
AB = DC
−−>
AB = [5, 3]
−−>
DC = [4 − xd, 5 − yd]
5 = 4 − xd / −5 + xd
3 = 5 − yd /−3 + yd
xd = −1
yd = 2
D = ( −1, 2) mamy D (niebieskie)
Długość |AB|
|AB| = √(5)2) + (3)2 = √25+9 = √34
Długość |BC|
|BC| = √(2)2) + (4)2 = √4+16 = √20 = 2 * √5
Długość przekątnej d (|DB|)
|DB| = √(3)2) + (−1)2 = √9+1 = √10
Twierdzenie cosinusów
10 = 20 + 34 − 2 * √34 * √20 * cosα
10 = 54 − 2 * √680 *cosα / −10 + 2 * √680 * cosα
2 * √680 * cosα = 44 / : 2
√680 * cosα = 22 / : √680

 Wierzchołek D i pole równoległoboku wyznaczyłeś poprawnie. Do sposobu wyznaczenia
wierzchołka D nie mam uwag, natomiast pole wyznaczyłeś w najgorszy możliwy sposób,
tracąc przy tym dużo czasu. Łatwiej i zdecydowanie prościej wyznacza się pole równoległoboku
następująco:
A = (−3, −2), B = (2, 1), C = (4, 5), D = (−1, 2)
→
AB = [5, 3]
→
AD = [2, 4]
| 5 3 |
Pole P = | | | | = |20 − 6| = 14 [j2]
| 2 4 |
Proste i łatwe, prawda?
Wierzchołek D i pole równoległoboku wyznaczyłeś poprawnie. Do sposobu wyznaczenia
wierzchołka D nie mam uwag, natomiast pole wyznaczyłeś w najgorszy możliwy sposób,
tracąc przy tym dużo czasu. Łatwiej i zdecydowanie prościej wyznacza się pole równoległoboku
następująco:
A = (−3, −2), B = (2, 1), C = (4, 5), D = (−1, 2)
→
AB = [5, 3]
→
AD = [2, 4]
| 5 3 |
Pole P = | | | | = |20 − 6| = 14 [j2]
| 2 4 |
Proste i łatwe, prawda?
 może zapamiętam Twój sposób.
może zapamiętam Twój sposób.
 ale juz tego zmieniac nie będę
ale juz tego zmieniac nie będę
 Dobranoc Wszystkim
Dobranoc Wszystkim
 Tea Dobranoc
Tea Dobranoc
 Dobranoc
Dobranoc

 chyba dobrze cos105o * cos75o. to poprostu to samo tylko ze przy 105 będzie minus
ale potem i tak jest dodatni, Tak?
chyba dobrze cos105o * cos75o. to poprostu to samo tylko ze przy 105 będzie minus
ale potem i tak jest dodatni, Tak?
 bo nie zasnę
bo nie zasnę 
 oczywiście bez 12 w drugiej linijce!
oczywiście bez 12 w drugiej linijce!

 ok.
ok. 





 Dobranoc! Miłych snów
Dobranoc! Miłych snów

 Idę zatem spokojnie spać
Idę zatem spokojnie spać Dobranoc!
Dobranoc!
 po przekształceniu są to
te same funkcje tylko przy tej gdzie jest 105o będzie minus.
Można nawet sprawdzić na kalkulatorze, że cos105o to
Liczba −0,288, a cos 75o to liczba +0,288. wydaje mi się
Więc że się nie myliłem Bogdanie
po przekształceniu są to
te same funkcje tylko przy tej gdzie jest 105o będzie minus.
Można nawet sprawdzić na kalkulatorze, że cos105o to
Liczba −0,288, a cos 75o to liczba +0,288. wydaje mi się
Więc że się nie myliłem Bogdanie tylko do końca tego nie
Przemyślałem
tylko do końca tego nie
Przemyślałem
 xD
xD


 to świetnie
to świetnie No tak dziś jest super upalnie aż do teraz
No tak dziś jest super upalnie aż do teraz