:)
Fan: Dla jakich wartości parametru k i p równanie |(x−2)2+k|=p ma dokładnie trzy rozwiązania?
9 lut 15:01
MQ:
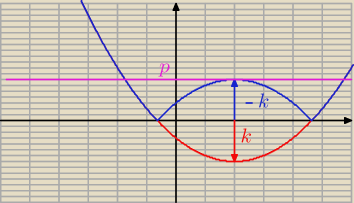
9 lut 15:15
Fan: thx
9 lut 15:16
Bogdan:
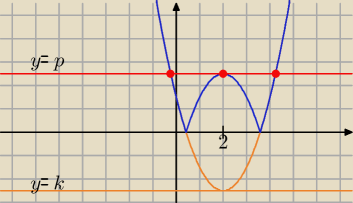
Rysunek ilustruje zagadnienie i podpowiada odpowiedź
pomarańczowa krzywa: y = (x − 2)
2 + k
niebieska krzywa: y = |(x − 2)
2 + k|
9 lut 15:17
pigor: ..., otóż widzę to tak :
warunki zadania spełnia parabola funkcji y=(x−2)
2 przesunięta o parametr
k do dołu , czyli parabola y=(x−2)
2+k i
k<0 , której część ujemną ,
wartość bezwzględna, odbija względem osi OX tak, że krzywa
y=|(x−2)2+k| = p ma dokładnie 3 rozwiązania ⇔
p=|k| i k<0 ⇔
⇔
p=−k i k<0 ⇔
p+k=0 i k<0 i to byłoby tyle ...
9 lut 15:32
pigor: .. O
, grzebałem się online, a tu proszę , piękne rysunki już dawno były . ...
9 lut 15:35
Fan: dzięki wielkie
9 lut 15:45