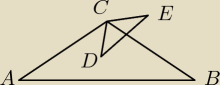
Trójkąt ABC i CDE są równoramienne, |AC| = | BC|, |CD| = |CE| oraz |kąt ACB| = | Rejn: Trójkąt ABC i CDE są równoramienne, |AC| = | BC|, |CD| = |CE| oraz |kąt ACB| = |kąt DCE|. Wykaż, że |AD| = |BE|. Bardzo potrzebuje a nie potrafię za bardzo. Z góry dzieki.

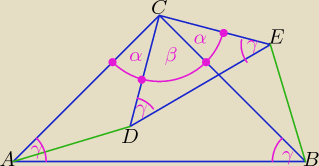
Bogdan: Każdy z trójkątów ADC i BEC ma boki tej samej długości: AC w trójkącie ADC i BC w trójkącie BEC oraz CD w ΔADC i CE w ΔBEC, miary katów między tymi bokami też są sobie równe: |∡ACD| = |∡BCE| = α, stąd wnioskujemy, że te dwa trójkąty: ΔADC i ΔBEC są przystające na podstawie cechy przystawania bkb (bok kąt bok), wobec tego równej długości są boki AD i BE.

dlaczego: Dlaczego kąt acd i bce są równe?