Zadania dla Kuby, zestaw 3 Bogdan: Zadania dla Kuby, zestaw 3. 1. Kolejne boki czworokąta wpisanego w okrąg mają długości: 3, 5, 6, 9. Wyznacz cosinus kąta między najkrótszymi bokami. 2. Znajdź punkt symetryczny do punktu A = (2, 6) względem prostej o równaniu 3x + 4y − 5 = 0. 3. Wycinek koła przy zwinięciu utworzył powierzchnię boczną stożka, którego kąt rozwarcia jest prosty. Wyznacz miarę kąta środkowego tego wycinka.

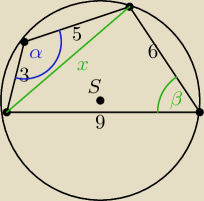
Kuba: Zadanie 1. Dane 3, 5, 6, 9 − to długości boków tego czworokąta wpisanego w okrąg S − środek okręgu α − szukamy cos tego kąta β − wartość tego kąta wynosi (180^o − α) Korzystam z Twierdzenia cosinusów x² = 3² + 5² − 2 * 3 * 5 * cosα x² = 6² + 9² − 2 * 6 * 9 * cos(180^o − α) <−−−−stosuje wzór redukcyjny cos(180^o − α) = − cosα x² = 9 + 25 − 30 * cosα x² = 36 + 81 − 108 * (−cosα) x² = 34 − 30 * cosα x² = 117 − 108 * (−cosα) x² = 34 − 30 * cosα x² = 117 + 108 * cosα 34 − 30 * cosα = 117 + 108 * cosα / −34 − 30 * cosα = 83 + 108 * cosα /+ 30 * cosα 83 + 138 * cosα = 0 138 * cosα = (−83) cosα = −0,601 nie wiem co mam zrobić z tym minusem

Bogdan: Zadanie rozwiązałeś poprawnie. Należało uzasadnić fakt: β = 180^o − α powołując się na twierdzenie o czworokącie wpisanym w okrąg (brak tego uzasadnienia może skutkować nie przyznaniem 1 punktu). Jeśli w zadaniu nie ma wyraźnego polecenia o podaniu wyniku z określoną dokładnością, to nie zamienia się ułamków zwykłych na dziesiętne. Rozwiązanie

	83
należało zakończyć odpowiedzią: cos α = −		.
	138

Znak minus oznacza, że kąt α jest rozwarty i zawiera się w przedziale (90^o, 180^o), cosinus kąta w drugiej ćwiartce jest ujemny.

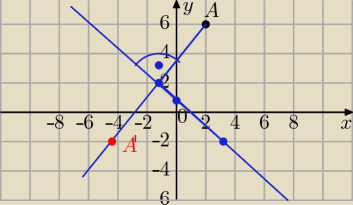
Kuba: A = (2, 6) 3x + 4y − 5 = 0 / −4y −4y = 3x − 5 / :{−4)

	3		5
y=(−		x) +
	4		4

niebieska linia to wykres tej prostej Liczymy odległość punktu p od prostej y Wzór:

	|Ax0 + By0 + C|
	√A2 + B2

prosta 3x + 4y − 5 = 0 Ax + By + C = 0 A = (2, 6) A = (x₀, y₀) Podstawiamy

|3*2 + 4*6 − 5|		|6 + 24 − 5|		25		25
	=		=		=		= 5
√32 + 42		√9 + 16		√25		5

Odległość punktu A od prostej y wynosi 5. Nie wiem jak teraz to zrobić Ja odmierzyłem taką samą długość po drugiej stronie prostej prostopadle do niej, odczytałem ile wynosi punkt A'=(−2, −4) i Teraz za pomocą tego wzoru na odległość sprawdzam czy się zgadza odległość A' od prostej.

|3*−4 + 4*−2 − 5|		|−12− 8− 5|		|−25|		25
	=		=		=		=5
√32 + 42		√9 + 16		√25		5

Odp.: Punkt symetryczny do punktu A = (2, 6) względem prostej o równaniu 3x + 4y − 5 = 0, wynosi A'=(−4, −2).

Kuba: ahha oo to super dobrze że tyle mi się udało zrobić i dziękuje za kolejne wskazówki.

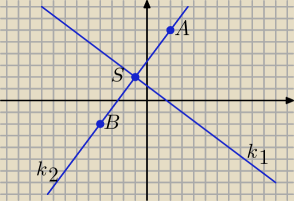
Bogdan: Ad. zad. 2. Kubo, nie podaje się w rozwiązaniu wzorów, które są umieszczone w broszurce z wzorami dołączanej do arkusza maturalnego podczas egzaminu maturalnego. Np. w tym zadaniu

	|3*2 + 4*6 − 5|
wystarczyło napisać: d =		= 5.
	√9 + 16

Zadanie można rozwiązać na kilka sposobów, przedstawię jeden z nich, który nie wymaga obliczania długości d. Zadanie. Znajdź punkt symetryczny do punktu A = (2, 6) względem prostej o równaniu 3x + 4y − 5 = 0. Rozwiązanie. A = (2, 6), B = (x_B, y_B) to punkt symetryczny do A względem prostej k₁, S = (x_S, y_S) to punkt wspólny prostych k₁ i k₂ będący środkiem odcinka AB.

	3		5
prosta k1: 3x + 4y − 5 = 0 ⇒ y = −		x +		, S ∊ k1,
	4		4

prosta k₂: y = a₂x + b₂, A ∊ k₂, B ∊ k₂

	3		4
k2 ⊥ k1 ⇔ a2 * −		= −1 ⇒ a2 =
	4		3

	4		8		10
k2: y = a2x + b2 i A ∊ k2 ⇒ 6 =		*2 + b2 ⇒ b2 = 6 −		=
	3		3		3

	4		10
k2: y =		x +
	3		3

Wyznaczamy punkt S przez porównanie wzorów prostych k₁ i k₂.

	3		5		4		10
−		x +		=		x +		/ *12 ⇒ −9x + 15 = 16x + 40 ⇒ 25x = −25 ⇒ x = −1
	4		4		3		3

	4		10
i y =		* (−1) +		= 2
	3		3

S = (−1, 2)

	xB + 2
Punkt S jest środkiem odcinka AB, więc		= −1 ⇒ xB = −4,
	2

	yB + 6
		= 2 ⇒ yB = −2
	2

B = (−4, −2) Odp.: Punkt symetryczny do punktu A = (2, 6) względem prostej o równaniu 3x + 4y − 5 = 0 to punkt B = (−4, −2)

Kuba: Zadanie 3 Dane: na zielono zaznaczony wycinek koła (z którego zrobiona jest powierzchnia boczna stożka) o kącie szukanym α H − na czerwono zaznaczona jest wysokośc stożka r − na pomarańczowo promień podstawy stozka l − tworząca stozka β − kąt w trójkącie prostokątnym równoramiennym wynosi 45^o (czarne kąty) 2β − kąt rozwarcia (90^o) Jeżeli kąty są równe to długości boków(h i r) tego trójkąta prostokątnego są równe H = r Licze z pitagorasa l(tworzącą) Wzór: l = √H² + r² l = H * √2 Czyli moge obliczyć Pole powierzchni bocznej: Wzór P = π * r * l P = πH² * √2 i pożniej Korzystam z https://matematykaszkolna.pl/strona/1004.html licze α ze wzoru na P_b Znając Pole boczne moge obliczyć α Korzystam z https://matematykaszkolna.pl/strona/1004.html wzór końcowy na α

	r * 360o
α =
	l

	H * 360o
α =
	H * √2

	360o
α =
	√2

α ≈ 254,6^o Odp. Szukany kąt środkowy wycinka tego koła wynosi α ≈ 254,6^o. Mam nadziele, że dobrze bo ten kąt jakiś dziwny wyszedł...

Kuba: ok a czy moja wersja zadania 2 mogłaby być tak przedstawiona na maturze?

Bogdan: Kubo, w zadaniu 2 poza wyznaczeniem odległości od punktu A do prostej nic więcej nie wyznaczyłeś, więc nie przedstawiłeś żadnej wersji rozwiązania. Co to znaczy: "odmierzyłem taką samą długość po drugiej stronie prostej prostopadle do niej, odczytałem ile wynosi punkt A'=(−2, −4) ". Jak Kubo odmierzyłeś?, linijką?, cyrklem? Wspominałem już, że odczytanie rozwiązania z rysunku nie może być uznane za rozwiązanie, rysunek jest tylko narzędziem wspomagającym i ilustracją rozwiązania.

Bogdan: Ad. zad. 3. Zabrakło ostatniego kroku.

	360o		360o * √2
α =		=		= √2*180o
	√2		2

Można było rozwiązać nieco prościej. L − długość tworzącej, R − długość promienia podstawy stożka, γ − miara kata rozwarcia stożka, β − miara kąta środkowego wycinka koła, z którego utworzono stożek

	γ		√2
γ = 90o,		= 45o, sin45o =		,
	2		2

R		γ		R		√2
	= sin		⇒		=
L		2		L		2

Obwód podstawy stożka = długość łuku wycinka koła,

	βo		R		βo		R
2πR =		*2πL ⇒		=		⇒ βo = 360o*		⇒
	360o		L		360o		L

	√2
⇒ βo = 360o*		= √2*180o
	2

Kuba: Hmmm no przyrządy można mieć na maturz, tu na oko ale wyszło dobrze wiec doszedłem do wyniki inna droga niz jest podana w kluczu(tak zakładam) więc zadanie powinno być wysoko punktowane za rozwiazanie innym sposobem. Ale moge się mylić...

Bogdan: Muszę Cię zmartwić. Nie doszedłeś do rozwiązania w zadaniu 2 i nie dostałbyś za to zadanie punktów. Nie przyznaje się punktów za brak rozwiązania, a takim jest uzyskanie odpowiedzi "na oko". Oceniana jest przez egzaminatora droga, która doprowadziła do wyniku. Takiej drogi u Ciebie nie ma. Odczytanie rozwiązania z rysunku przy braku takiego polecenia w zadaniu nie jest uznawane za rozwiązanie.

Kuba: Szkoda:( no ale ok. Będe sie starał je jakos liczyć normalnie matematycznie a jak nie bede potrafił to napisze.