Problem Kipic: dla jakiej wartosci parametru m rozwiazaniem rownania lx−1l = m+ 2 jest para liczb o przeciwnych znakach; nie jest to funkcja kwadratowa wiec nie moze byc zlozen z delta x₁ i x₁ prosze o pomoc bo niemam pojecia jak to zrobic dla funkcji liniowej

Kipic: prosze o jakies wskazowki

Dominik: narysuj f(x) = |x − 1| i przecinaj to prosta g(x) = m + 2. dla jakich m prosta przecina sie w x o roznych znakach?

jikA: Można też zrobić wykorzystując wzory Viete'a. |x − 1| = m + 2 / ² zał. m + 2 ≥ 0 (x − 1)² = (m + 2)² x² − 2x + 1 = m² + 4m + 4 x² − 2x − m² − 4m − 3 = 0 x₁x₂ < 0

− m2 − 4m − 3
	< 0
1

m² + 4m + 3 > 0 (m + 1)(m + 3) > 0 ⇒ m ∊ (−∞ ; −3) ∪ (−1 ; ∞) ∧ m ∊ [−2 ; ∞) ⇒ m ∊ (−1 ; ∞) Trochę naokoło ale da się zrobić.

jikA: Inny sposób najłatwiejszy to zauważyć że funkcja f(x) = |x − 1| przecina oś OY w punkcie A (0 ; 1) tak więc warunki zadania będą spełnione kiedy m + 2 ≥ 0 ∧ m + 2 > 1 ⇒ m ∊ (−1 ; ∞).

Kipic: dziekuje slicznie

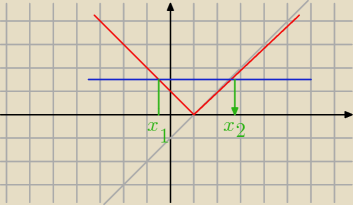
Aga1.: Graficznie y=x−1 −−kolor szary y=Ix−1I −−kolor czerwony y=m+1 −−−niebieski Z wykresu widać, że m+2>1