Zadania dla Kuby. Bogdan: Zadania dla Kuby. 1. W dwunastościanie foremnym odcięto płaszczyznami przechodzącymi przez środki krawędzi każdy z narożników. Ile ścian ma powstała w ten sposób bryła i jakimi są one wielokątami.

	√5		π		3√10		π
2. Wiadomo, że sinα =		i α∊(0,		), cosβ =		i β∊(0,		).
	5		2		10		2

	π
Wykaż, że α + β =		.
	4

3. Liczby x₁, x₂ (x₁ ≠ x₂) są pierwiastkami równania kwadratowego x² + 2mx + m = 0. Narysuj wykres funkcji g określonej wzorem g(m) = x₁² + x₂².

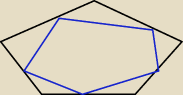
Kuba: 1. Odczytałem z rysunku: w każdym wierzchołku powstanie jeszcze dodatkowo 20 trójkątów równobocznych i pięciokąty ale pomniejszone tak jak na rysunku.(niebieski) Bryła która powstałą to trzydziestodwuścian

Kuba: zapomniałem dodać że pięciokąty foremne powstały(ten niebieski)

AD: Pomyliłeś dwunastościan z dwunastokątem.

Kuba: nic nie pomyliłem... na rysunku pkazałem tylko 1 ściane dwunastościanu http://pl.wikipedia.org/wiki/Dwunasto%C5%9Bcian_foremny

Bogdan: Kubo, brakuje kilku uzasadnień w Twoim rozwiązaniu, a także są nieścisłości: 1. Dlaczego rozpatrujesz pięciokąt foremny, a nie inną figurę? 2. Dlaczego powstają trójkąty równoboczne w wierzchołkach i dlaczego jest ich 20? 3. Dlaczego wewnątrz pięciokąta foremnego powstaje również pięciokąt foremny? 4. Nieścisłością jest stwierdzenie, że w każdym wierzchołku powstanie 20 trójkątów równobocznych, bo w każdym wierzchołku po jego ścięciu powstanie 1 trójkąt równoboczny. Popraw zapis rozwiązania i wykonaj porządny rysunek (masz przecież do dyspozycji przycisk z pięciokątem).

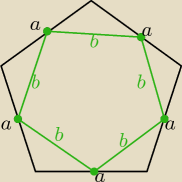
Kuba: Ad. 1. Rozpatruje pięciokąt foremny ponieważ dwunastościan Foremny jak sama nazwa wskazuje to wielościan foremny o 12 ścianach w kształcie pięciokątów foremnych. Ad.2 Jest ich dwadzieścia ponieważ tyle jest wierzchołków. Można zastosować wzór Eulera: s − k + w = 2 s − liczba ścian (w tym wypadku 12) k − liczba krawędzi (w tym wypadku 30) w − liczba wierzchołków (w tym wypadku jeżeli Bogdanie nie chcesz znac ilości wierzchołków to je oblicze ) 12 − 30 + w = 2 −18 + w = 2 /+18 w = 20 każdy narożnik jest odcięty(20 narożników odcinamy płaszczyzną przechodzącą przez 3 środki krawędzi przy każdym narożniku. Powstają trójkąty równoboczne o wszystkich krawędziach równych długości odcinka łączącego dwie sąsiednie krawędzie pięciokąta foremnego. Ad.3 Powstają pieciąkąty foremne(zielony) o wszystkich krawędziach równych długości odcinka łączącego dwie sąsiednie krawędzie pięciokąta foremnego(czarny). Ad. 4 żle napisałem, ale miałem na myśli że w każdym ściętym wierzchołku powstanie 1 trójkąt równoboczny, za błąd przepraszam

Kuba: Mam nadzieje że wszystko już jest ok

Kuba: Zadanie 2 ^π₂ = 90^{o π}₄ = 45^o sinα ^√5₅ ≈ 0,447 ≈ 26^o α ≈ 26^o α ∊ (0, 90^o) cosβ ^3√10₁₀ ≈ 0,949 ≈ 19^o β ≈19^o β ∊ (0, 90^o) α + β = 45^o α + β = 26^o + 19^o = 45^o

Bogdan: Teraz jest dobrze, chociaż twierdzenia Eulera nie było potrzeby tu przywoływać. Wystarczyło stwierdzić: Ściany dwunastościanu foremnego są pięciokątami foremnymi. Dwunastościan foremny posiada 20 wierzchołków, każdy narożnik tej bryły jest wierzchołkiem trzech ścian (pięciokątów foremnych), przekrój każdego naroża płaszczyzną określoną warunkami zadania jest trójkątem równobocznym, jest więc 20 ścian będących trójkątami równobocznymi. Płaszczyzny przekroju wycinają z każdej ze ścian dwunastościanu foremnego pięciokąt foremny. Jest więc w powstałej z dwunastościanu foremnego po ścięciu jego narożników 12 ścian będących pięciokątami foremnymi i 20 ścian w kształcie trójkątów równobocznych, razem bryła posiada 32 ściany. Jeśli chodzi o nieścisłość, to egzaminator sprawdzający Twoją pracę słów usprawiedliwienia i przeprosin nie zobaczyłby. Rysunek jest teraz porządny.

Bogdan: Niestety, zadanie drugie nie jest poprawnie rozwiązane. Nie przechodzimy na miarę stopniową. Nie stosujemy przybliżeń liczb. Potrzebny jest w tym zadaniu inny pomysł na jego rozwiązanie. .

Kuba: rozumiem. a w zadaniu 2 nie rozumiem dlaczego nie moge przejśc na miarę stopniową przeciez w zadaniu pisze tylko wykaż, a nie wykaż nie używając miary stopniowej i przybliżeń liczb. Nie wiem jak to inaczej rozwiązać.

.: 3.(x₁+x₂)²−2x₁x₂

.: (−b/a)²−2(c/a)=0 (−2m)²−2m=0 4m²−2m=0 2m(2m−1)=0 m=0 i m=1/2

.: zmien nick z łaski swojej

.: y=x² y=x²+x+1/2=0 2 wykresy i część wspólna

.: heh

.: ktos mnie przesladuje juz 2 raz dowiem sie kto?

.: próbuje razem z Tobą ale nie wiem czy to dobrze

.: heh fajnie to jzu 2 raz robis znie

.: a tam zobaczymy jak Bogdan poprawi

.: ale mam racje?

Bogdan: Ad. zad. 2. Jeżeli w zadaniu miary kątów są podane w mierze łukowej, to nie przechodzi się na inną miarę, np. stopniową, przyjmij to jako zasadę przy rozwiązywaniu zadań. Zauważmy, że jeśli miary katów α i β należą do pierwszej ćwiartki, to sinα > 0, cosα > 0, sinβ > 0 i cosβ > 0.

	√5		2√5
sinα =		⇒ cosα = √1 − sin2α = √1 − 5/25 = √20/25 =		.
	5		5

	3√10		√10
cosβ =		⇒ sinβ = √1 − cos2β = √1 − 90/100 = √10/100 =		.
	10		10

Korzystamy z zależności: sin(α + β) = sinαcosβ + sinβcosα.

	√5		3√10		√10		2√5		5√50
sin(α + β) =		*		+		*		=		=
	5		10		10		5		50

	25√2		√2
=		=
	50		2

	√2		π		π		π
sin(α + β) =		⇒ sin(α + β) = sin		⇒ α + β =		dla α, β ∊ (0,		)
	2		4		4		2

co należało wykazać.

.: yeah

.: no bylam bliskoxD

.: a to 2 ja chce 3!

.: ja tez

.: fajnie..

.: prosimy o wytłumaczenie 3 zadania

Kuba: g(m) = x₁² + x₂² = (x₁ + x₂)² − 2x₁ * x₂ (wzór skróconego mnożenia) wzory Viete'a g(m) = (−^b_a)² − 2* ^c_a podstawiamy z: x² + 2mx + m = 0 a = 1 b = 2m c = m a = 1 czyli może zapisać tak: g(m) = b² − 2c = 4m² − 2m = 2m(2m−1) jest to funkcja kwadratrowa z miejscami zerowymi 0 i 0,5

.: x₁+x₂=−b/a x₁*x₂=c/a

.: o a chcialam zrobic

Kuba: łooo ktoś już doszedł do tego

.: ?

Kuba: to narysuj wykres

Kuba: o 16:20 już Ty albo ten drugi ".:" to napisał

...: nom doszedł gorzej z wykresem

.: kto Ty jestes ;

.: czemu 2 raz mnie przesladujesz

...: sorry już się nie wtrącam pozdrawiam!

.: ale kto Ty powiedz

.: z/w

Bogdan: Ad. zad. 3. W podanych tu rozwiązaniach brakuje pewnych zapisów, ich brak z pewnością obniży punktację za rozwiązanie. Poprawne rozwiązanie jest następujące: Równanie kwadratowe: x² + 2mx + m = 0 ma dwa różne pierwiastki ⇔ Δ > 0. Δ = 4m² − 4m > 0 ⇒ 4m(m − 1) > 0 ⇒ m ∊ (−∞, 0) U (1, +∞) + + + + + + −−−−−−−−−−−−−−(0)−−−−−−−−−−−−(1)−−−−−−−−−−−−−> − − − x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂ Po zastosowaniu wzorów Viete'a otrzymujemy: x₁² + x₂² = 4m² − 2m. g(m) = 4m² − 2m, m ∊ ℛ.

	1		1
Wierzchołek paraboli W(mw, gw) = (		, −		)
	4		4

	2		1		1		1		1		1
mw =		=		, gw = g(		) = 4*		− 2*		= −
	8		4		4		16		4		4

Uwzględniając ograniczenie dla m mamy: g(m) = 4m² − 2m, D_g: m ∊ (−∞, 0) U (1, +∞) Uwaga: Odcięta m_w wierzchołka paraboli g = 4m² − 2m nie należy do D_g. Najpierw szkicujemy delikatną linią wykres g = 4m² − 2m, potem pogrubiamy tę część wykresu, która odpowiada m ∊ (−∞, 0) U (1, +∞).

Kuba: Nie rozumiem Bogdanie jak obliczyłeś g_w?

Kuba: aaaa już wiem

Bogdan: Przy okazji ostatniego zadania wtrącę następującą uwagę. Jeśli dana jest funkcja kwadratowa w postaci: a) ogólnej: f(x) = ax² + bc + c, to wierzchołek paraboli W(x_w, y_w) można wyznaczyć tak:

	b
xw = −
	2a

	Δ
yw = −		lub yw = f(xw) = a*xw2 + b*xw + c lub yw = c − a*xw2.
	4a

b) w postaci iloczynowej dla Δ > 0: f(x) = a(x − x₁)(x − x₂), to:

	x1 + x2
xw =		,
	2

y_w = a*(x_w − x₁)*(x_w − x₂)

Kuba: super Bogdan a Ty się na wakacje nie wybierasz?;>

Bogdan: Nie, jestem w okresie wakacji w domu.

Kuba: o to super.

Kuba: jak będziesz miał czas to prosze wrzuć wiecej zadań bo te juz jak widać rozwiązane i przedystkutowane

Bogdan: Dobrze, za chwilę przekażę następne 3 zadania. Mam prośbę do Ciebie. Przedstawiaj swoje rozwiązania w taki sposób, jakbyś zdawał prawdziwą maturę. Oczekuję pełnych rozwiązań zawierających wszystkie uzasadnienia. Rozwiązanie każdego zadania kończ pełną odpowiedzią.

Kuba: Będę się starał tak je przedstawiać