Oblicz stosunek pól dwóch figur Kobra: W trapezie ABCD (ABIICD) dwusieczna kąta wewnętrznego ABC jest prostopadła do ramienia AD trapezu i ma z tym ramieniem punkt wspólny P. Punkt P dzieli ramię AD w stosunku 2:1, licząc od wierzchołka A. Oblicz stosunek pola trójkąta ABP do pola czwaorokąta PBCD

M:

M:

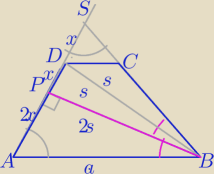Mila: x− wspólna miara, x>0 1) dwusieczna BP ⊥AD i BP⊥AS w ΔASB Δ ASB− Δ równoramienny, |PS|=2x P_ΔABS=4s P_ΔABP=2s P_PBCD=P_ΔPBS−P_ΔDCS=2s−P_ΔDCS 2)

	x		1
ΔDCS∼ΔABS w skali k=		=
	4x		4

	1		1
PΔDCS=		*4s=		s
	16		4

	1		7
PPBCD=2s−		s=		s
	4		4

3)

PABP		2s		8
	=		=
PPBCD		7   s 4		7

========================