 Witam, gdzie robię błąd?
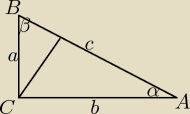
W trójkącie prostokątnym ABC przyprostokątne mają długości |AC| = b, |BC| = a, wysokość
opuszczona z wierzchoła kąta prostego ma długość h. Wykaż, że jezeli b2 = ah to cos∡BAC =
Witam, gdzie robię błąd?
W trójkącie prostokątnym ABC przyprostokątne mają długości |AC| = b, |BC| = a, wysokość
opuszczona z wierzchoła kąta prostego ma długość h. Wykaż, że jezeli b2 = ah to cos∡BAC =
| √5 − 1 | ||
. | ||
| 2 |
| b | √5 − 1 | |||
cosα = | = | |||
| c | 2 |
| √5 − 1 | 3 − √5 | |||
( | )2 = | |||
| 2 | 2 |
| ah | 3 − √5 | ||
= | − cos2α zgodnie z tw. pitagorasa i b2=ah | ||
| a(a + h) | 2 |
| h | 3 − √5 | ||
+ 1= | |||
| a | 2 |
| h | 1 − √5 | ||
= | = sinβ=cosα | ||
| a | 2 |
| √5 − 1 | ||
Cosinus ujemny jest równy dodatniemu, czyli to będzie | ? Proszę o odowiedź. | |
| 2 |
| h | b | |||
Czy sinβ = | = | ? | ||
| a | c |
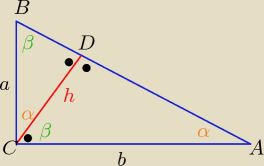 α€(0o,90o), cosα>0
Trójkąty CAD i CDB są podobne z cechy (kkk)
α€(0o,90o), cosα>0
Trójkąty CAD i CDB są podobne z cechy (kkk)
| b2 | ||
z treści zadania :b2=ah ⇒ a= | ||
| h |
| h | h | h2 | h | |||||||||||
wΔCDB cosα= | = | = | = ( | )2= sin2α | ||||||||||
| a |
| b2 | b |