 Dziękuje Bogdanie
Dziękuje Bogdanie zamienie mój nick z b na Kuba
Prosze o szczegółowe tłumaczenie krok po kroku tego czego nie rozumiem.
Z góry dziękuje
Również z góry przepraszam za błędy nawet językowe i prosze o poprawianie
zamienie mój nick z b na Kuba
Prosze o szczegółowe tłumaczenie krok po kroku tego czego nie rozumiem.
Z góry dziękuje
Również z góry przepraszam za błędy nawet językowe i prosze o poprawianie Od dziś będę wchodził tu bardzo często
Od dziś będę wchodził tu bardzo często 1.
1.−x2 + 4x = m
−x2 + 4x − m = 0 / *(−1)
x2 − 4x + m = 0
żeby otrzymać 2 pierwiastki Δ>0
a = 1
b = −4
c = m
x1 > 1
x2 > 1
x1 − 1 > 0
x2 − 1 > 0
nie mam pomysłu
1.
1.−x2 + 4x = m
−x2 + 4x − m = 0 / *(−1)
x2 − 4x + m = 0
żeby otrzymać 2 pierwiastki Δ>0
a = 1
b = −4
c = m
x1 > 1
x2 > 1
x1 − 1 > 0
x2 − 1 > 0
nie mam pomysłu 2.
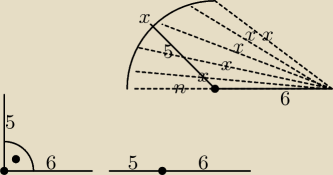
Przerywana − to możliwa długość tego boku
x − długość tego boku , w tym wypadku w przedziale liczbowym
Wiemy że napewno przedział liczbowy (wartość tego najdłuższego boku w tym trójkącie
rozwartokątnym) będzie obustronnie otwarty, ponieważ długość tego boku nie może wynosić:
5 + 6 = 11 musi być mniejszy (bo inaczej by się linie pokrywały i nie było by mowy o trójkącie)
od 11 czyli x<11
z pitagorasa obliczamy przeciwprostokątną(z)
52 + 62 = z2
25 + 36 = 61
z= √61
czyli x>z poniewaz x nie może wynosić tyle ile wynosi przeciwprostokątna bo był by to trójkąt
prostokątny
x∊(√61, 11)
3.log a = −3, log b = 2
log (a3 * b4) = log a3 + log b4 ( skorzystałem ze wzoru: loga x + loga y = loga
(x*y) )
log a3 + log b4 = 3*log a + 4*log b ( skorzystałem : loga xp = p*loga x )
3*log a + 4*log b = 3 * (−3) + 4 * 2 = (−9) + 8 = (−1)
czyli log (a3 * b4) = (−1) = log 10−1 więc a3 * b4 = 10−1 = 0,1
2.
Przerywana − to możliwa długość tego boku
x − długość tego boku , w tym wypadku w przedziale liczbowym
Wiemy że napewno przedział liczbowy (wartość tego najdłuższego boku w tym trójkącie
rozwartokątnym) będzie obustronnie otwarty, ponieważ długość tego boku nie może wynosić:
5 + 6 = 11 musi być mniejszy (bo inaczej by się linie pokrywały i nie było by mowy o trójkącie)
od 11 czyli x<11
z pitagorasa obliczamy przeciwprostokątną(z)
52 + 62 = z2
25 + 36 = 61
z= √61
czyli x>z poniewaz x nie może wynosić tyle ile wynosi przeciwprostokątna bo był by to trójkąt
prostokątny
x∊(√61, 11)
3.log a = −3, log b = 2
log (a3 * b4) = log a3 + log b4 ( skorzystałem ze wzoru: loga x + loga y = loga
(x*y) )
log a3 + log b4 = 3*log a + 4*log b ( skorzystałem : loga xp = p*loga x )
3*log a + 4*log b = 3 * (−3) + 4 * 2 = (−9) + 8 = (−1)
czyli log (a3 * b4) = (−1) = log 10−1 więc a3 * b4 = 10−1 = 0,1
| −b | ||
p= | =2
| |
| 2a |

| −b | ||
wierzchołka wykresu tej funkcji, czyli paraboli wyraża się wzorem: xw = | . | |
| 2a |
| −b | −b | |||
4. | > p lub | < q | ||
| 2a | 2a |
| −b | 4 | |||
4. | > 0 ⇒ | > 0 ⇒ m ∊ ℛ | ||
| 2a | 2 |
 Zadanie 1, sposób 2.
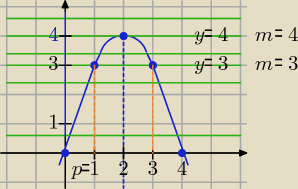
Równanie: −x2 + 4x = m.
Mamy tu 2 wykresy:
y = −x2 + 4x (parabola) oraz y = m (linia prosta będąca wykresem funkcji stałej).
Wierzchołek paraboli W(xw, yw) = (2, 4).
Prosta y = m może znajdować się w różnym położeniu (zielona linia). Szukamy takiego jej
położenia, w którym przecinać będzie parabolę w dwóch punktach, odcięte tych punktów
są większe od 1 (x1 > 1 i x2 > 1).
Takie położenie prosta y = m przyjmuje dla m ∊ (3, 4).
Dodam na zakończenie uwag do zadania 1, że podczas matury należy zastosować
sposób 1, a sposób 2 można dołączyć, ale tylko jako ilustrację rozwiązania.
Podkreślam, że sposób 2 nie jest analitycznym rozwiązaniem i formalnie nie może być
uznany za pełne rozwiązanie zadania.
Zadanie 1, sposób 2.
Równanie: −x2 + 4x = m.
Mamy tu 2 wykresy:
y = −x2 + 4x (parabola) oraz y = m (linia prosta będąca wykresem funkcji stałej).
Wierzchołek paraboli W(xw, yw) = (2, 4).
Prosta y = m może znajdować się w różnym położeniu (zielona linia). Szukamy takiego jej
położenia, w którym przecinać będzie parabolę w dwóch punktach, odcięte tych punktów
są większe od 1 (x1 > 1 i x2 > 1).
Takie położenie prosta y = m przyjmuje dla m ∊ (3, 4).
Dodam na zakończenie uwag do zadania 1, że podczas matury należy zastosować
sposób 1, a sposób 2 można dołączyć, ale tylko jako ilustrację rozwiązania.
Podkreślam, że sposób 2 nie jest analitycznym rozwiązaniem i formalnie nie może być
uznany za pełne rozwiązanie zadania.
 Dużą rolę w ocenie rozwiązania ma jego sposób zapisu i załączone ilustracje. Zapisy muszą
być poprawne językowo, bez błędów ortograficznych i gramatycznych, czytelne (chodzi
o charakter pisma, nie mogą być bazgroły, powinny być dość duże litery i inne symbole, nie
zgniecione zapisy ułamków, bez żadnych ozdobników i pochyleń, np. co innego oznacza
pionowa kreska |, a co innego ukośna w jedną stronę / i ukośna w drugą stronę \). Ale przede
wszystkim zapisy muszą być jasne, zrozumiałe, logiczne, spójne, każde następny zapis powinien
wynikać z poprzednich. Egzaminator i każdy sprawdzający naszą pracę po pierwszym
spojrzeniu na arkusz powinien odnieść pozytywne wrażenie estetyczne. Praca brzydko
napisana, z wieloma nieładnymi przekreśleniami, zmuszająca czytającego do wzrokowego
wysiłku, bo literki, cyferki i inne znaki są małe − takiego pozytywnego wrażenia nie zapewnia.
Każde zadanie powinno zawierać odpowiedź. Każdy rysunek powinien być staranie opisany.
Każde wprowadzone oznaczenie literowe powinno być opisane lub w ostateczności
pokazane na dołączonym do rozwiązania rysunku. Sprawdzający nie może tracić czasu
na odszyfrowywanie rozwiązania i nie powinien zastanawiać się i zgadywać, co autor
miał na myśli.
Starczy tych ogólnych uwag, chociaż można by jeszcze co nieco dodać, przejdźmy teraz
do zadania 2.
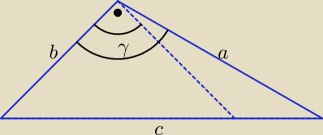
Zadanie 2.
a = 6, b = 5.
90o < γ < 180o.
Szukamy długości c, c > 0.
1. Z warunku trójkąta otrzymujemy: c < 5 + 6 = 11
2. Jeśli trójkąt jest rozwartokątny, to uwzględniając przyjęte oznaczenia mamy:
a2 + b2 < c2.
Stąd c > √a2 + b2 ⇒ c > √36 + 25 = √61
Odp.: Długość najdłuższego boku trójkąta c ∊ (√61, 11).
Dużą rolę w ocenie rozwiązania ma jego sposób zapisu i załączone ilustracje. Zapisy muszą
być poprawne językowo, bez błędów ortograficznych i gramatycznych, czytelne (chodzi
o charakter pisma, nie mogą być bazgroły, powinny być dość duże litery i inne symbole, nie
zgniecione zapisy ułamków, bez żadnych ozdobników i pochyleń, np. co innego oznacza
pionowa kreska |, a co innego ukośna w jedną stronę / i ukośna w drugą stronę \). Ale przede
wszystkim zapisy muszą być jasne, zrozumiałe, logiczne, spójne, każde następny zapis powinien
wynikać z poprzednich. Egzaminator i każdy sprawdzający naszą pracę po pierwszym
spojrzeniu na arkusz powinien odnieść pozytywne wrażenie estetyczne. Praca brzydko
napisana, z wieloma nieładnymi przekreśleniami, zmuszająca czytającego do wzrokowego
wysiłku, bo literki, cyferki i inne znaki są małe − takiego pozytywnego wrażenia nie zapewnia.
Każde zadanie powinno zawierać odpowiedź. Każdy rysunek powinien być staranie opisany.
Każde wprowadzone oznaczenie literowe powinno być opisane lub w ostateczności
pokazane na dołączonym do rozwiązania rysunku. Sprawdzający nie może tracić czasu
na odszyfrowywanie rozwiązania i nie powinien zastanawiać się i zgadywać, co autor
miał na myśli.
Starczy tych ogólnych uwag, chociaż można by jeszcze co nieco dodać, przejdźmy teraz
do zadania 2.
Zadanie 2.
a = 6, b = 5.
90o < γ < 180o.
Szukamy długości c, c > 0.
1. Z warunku trójkąta otrzymujemy: c < 5 + 6 = 11
2. Jeśli trójkąt jest rozwartokątny, to uwzględniając przyjęte oznaczenia mamy:
a2 + b2 < c2.
Stąd c > √a2 + b2 ⇒ c > √36 + 25 = √61
Odp.: Długość najdłuższego boku trójkąta c ∊ (√61, 11).
 Hmmm nie wiem dlaczego nie zawija mi tekstu. Może ktoś pomoże? Może teraz mi się zawinie
Hmmm nie wiem dlaczego nie zawija mi tekstu. Może ktoś pomoże? Może teraz mi się zawinie Co do zadania 1 zapomniałem dodać miejsc zerowych, ale obliczyłem je, ale na p i q już nie
wpadłem w nocy
Co do zadania 1 zapomniałem dodać miejsc zerowych, ale obliczyłem je, ale na p i q już nie
wpadłem w nocy ale za to 2 sposobem rozwiązałem na kartce tylko nie wiem dlaczego wydawało
mi się za proste i zrezygnowałem
ale za to 2 sposobem rozwiązałem na kartce tylko nie wiem dlaczego wydawało
mi się za proste i zrezygnowałem dobrze wiedzieć że 1 zadanie należy rozwiązać 1 sposobem
podanym przez Ciebie, bo ja na maturze pewnie obliczyłbym 2 sposobem.
nie rozumiem założeń 3 i 4, przy 1 zadaniu 1 sposobem.
super że udało mi się zrobić zadanie 2 i 3.
Czy zadanie 3 wykonane moim sposobem jest dobrym rozwiązaniem?
I mam nadzieje że odczytałeś coś z tego zawijasa.
dobrze wiedzieć że 1 zadanie należy rozwiązać 1 sposobem
podanym przez Ciebie, bo ja na maturze pewnie obliczyłbym 2 sposobem.
nie rozumiem założeń 3 i 4, przy 1 zadaniu 1 sposobem.
super że udało mi się zrobić zadanie 2 i 3.
Czy zadanie 3 wykonane moim sposobem jest dobrym rozwiązaniem?
I mam nadzieje że odczytałeś coś z tego zawijasa.
 Ad. zad. 1. Nie potrzeba wyznaczać miejsc zerowych. Co do założeń, to narysuj szkic
paraboli przecinającej oś x w dwóch punktach, wprowadź na tej osi dwa
dodatkowe punkty: jeden o wartości p na lewo od x1, drugi o wartości q na
prawo od x2, zaznacz również na osi odciętą wierzchołka paraboli xw
i teraz patrząc na rysunek spróbuj zrozumieć założenia.
Ad. zad. 3. Dobrze rozwiązałeś to zadanie.
Ad. zad. 1. Nie potrzeba wyznaczać miejsc zerowych. Co do założeń, to narysuj szkic
paraboli przecinającej oś x w dwóch punktach, wprowadź na tej osi dwa
dodatkowe punkty: jeden o wartości p na lewo od x1, drugi o wartości q na
prawo od x2, zaznacz również na osi odciętą wierzchołka paraboli xw
i teraz patrząc na rysunek spróbuj zrozumieć założenia.
Ad. zad. 3. Dobrze rozwiązałeś to zadanie.