Problem Kipic: Zbadaj liczbe pierwiastkow rownania w zaleznosci od parametru m lx² −2x−3l=m tutaj sie robi taki samo robi jak w rozwiazywaniu nierownosci czy liczy x ₁ i x₂ ?

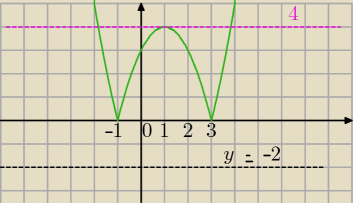
Tad: narysuj wykres f(x)=|x²−2x−3| i "tnij" ten wykes stałą y=m Ustalisz kiedy 0 ... kiedy 2 ... kiedy 4... kiedy 3... a kiedy znów 2 −

Mila: 1) x² −2x−3=0; Δ=4+12=16

	2−4		2+4
x1=		=−1 lub x2=		=3
	2		2

	2
xw=		=1
	2

|y_w|=|1−2−3|=4 Teraz szkic y=m 1) m<0 brak rozwiązań (czarny wykres y=−2 nie ma punktów wspólnych z f(x)] 2) m=0 2 rozwiązania 3) m∊(0;4) ...? 4)m=4 3 roz. 5)m>4 .... ? Uzupełnij

Kipic: dla m∊(0;4) beda 4 rozwiazania a dla m>4 bez zera hmmmm 2 wszystko jasne dzieki

Mila: Dla m>4 będą 2 rozwiązania ( co to zero ma znaczyć?) Możesz napisać jeden warunek: 2 rozwiązania dla m=0 lub m>4 pozostałe bez zmian.