parametr JoP: Dla jakich wartości parametru m równanie |m−2|=2m+1 ma a)jedno rozwiązanie b)dwa rozwiązania Wiem że założenie powinny wyglądać następująco a) 2m+1=0 b) 2m+1>0 mam tak w odpowiedzi ale nie wiem dlaczego tak ma to wyglądać?

JoP: Wie ktoś?

Tad: .. a widzisz tu jakiś parametr ... ja tu widzę równanie z niewiadomą m

JoP: sorki, powinno być tak |x−2|=2m+1

Tad: ... i jak to równanie pierwszego stopnia ... ma jedno rozwiązanie (m=1/3)

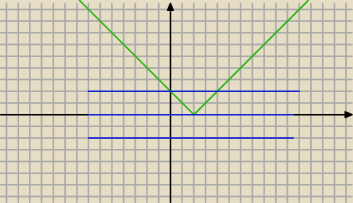
Tad: 2m+1<0 brak 2m+1=0 jedno 2m+1>0 dwa

JoP: jeśli już to całe równanie w a) ma m= − 0,5... Zadałem pytanie dlaczego tak mają wyglądać założenia, dlaczego nie jest liczone z całego równania, dlaczego licząc 2m+1>0 wychodzą dwa rozwiązania dla danego parametru?

Tad: ... a niby skąd to masz to swoje m=−0,5 ?

JoP: z odpowiedzi

Tad: bredzisz

JoP: ahaa...

JoP: pytam raz jeszcze dlaczego w tym zadaniu liczą tak (W ODPOWIEDZI, ROZWIĄZANIU) a)2m+1=0 b) 2m+1>0 a nie z całego równania? i dlaczego w przykładzie b) robiąc nierówność otrzymamy parametr dla którego równanie ma dwa rozwiązania?

Edyta PK: równanie to jest równaniem pierwszego stopnia, więc ma jedno rozwiązanie po pierwsze ustalamy wartość bezwzględną x−2 dla x−2>0 |x−2|={ −x+2 dla x−2<0 stąd x−2=2m+1 lub −x+2=2m+1 x=2m+3 x=−2m+1 więc 2m+3=−2m+1 m=−0,5

Edyta PK: to do podpunktu a) ma jedno rozwiązanie, gdy całe równanie przyrównamy do zera

Tad: ...o masz −:( Nie Edytko PK Równanie |x−2|=2m+1 ... ma ilość rozwiązań zależną od m

Tad: − dla 2m+1<0 czyli m<−1/2 ...układ jest sprzeczny ... więc nie ma rozwiązań − dla 2m+1=0 czyli m=−1/2 ...równanie ma jedno rozwiązanie − dla 2m+1>0 ...równanie ma dwa rozwiązania