prawdopodobieństwo Kin: w urnie jest 6 kul białych i 4 kule czarne. Do urny dołożono n kul białych. Wyznacz liczbę n jeśli wiadomo, że prawdopodobieństwo wylosowania dwóch kul białych jest teraz mniejsze od

	1
	2

Potrzebuje pomocy z rozwiązaniem tego zadania za pomocą drzewka bo mi dziwne wyniki wychodzą.

sushi_ gg6397228: zapisz swoje obliczenia, to sie sprawdzi

Basia: nie widzę tu zastosowania dla drzewka mamy 6+n białych i 4 czarne; razem 10+n losujemy dwie

	10+n 2		(10+n)!		(n+10)!
|Ω| =		=		=		=
			2!(8+n)!		2!(n+8)!

(n+9)(n+10)
2

A − obie białe

	6+n 2		(n+6)!		(n+5)(n+6)
|A| =		=		=
			2!(n+4)!		2

	(n+5)(n+6)   2
P(A) =		=
	(n+9)(n+10)   2

(n+5)(n+6)
(n+9)(n+10)

musisz rozwiązać nierówność

(n+5)(n+6)		1
	<
(n+9)(n+10)		2

mnożę przez 2(n+9)(n+10); mam prawo bo 2(n+9)(n+10)>0 2(n+5)(n+6) < (n+9)(n+10) a to już jest zwykła nierówność kwadratowa do rozwiązania

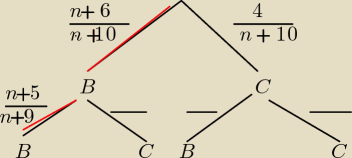
Mila: n+6 liczba B 4 liczba C n+10 liczba kul

	n+6		n+5
P(BB)=		*
	n+10		n+9

n+6		n+5		1
	*		<
n+10		n+9		2

n²+3n−30<0 i n∊N Δ=129

	−3−√129		−3+√129
n1=		<0 lub n2=		≈4,1
	2		2

n∊{0,1,2,3,4}