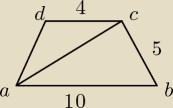
kilka zadań Seba_xD: Kilka zadań których nie mogę zrobić: 1.Długość przekątnej trapezu równoramiennego abcd przedstawionego na rysunku wynosi: A.2√29 B.√65 C.65 D.116 0 2.Do zbioru rozwiązań nierówności 2x(x−5)< bądź równe 0 należą: A.cztery liczby pierwsze B.Dwie liczby parzyste C.trzy liczby nieparzyste D.Cztery liczby naturalne 3.Podstawa AB trójkąta ABC leży na prostej o równaniu y=2x+5. Wysokość trójkąta poprowadzona z wierzchołka C=(3,1) zawiera się w prostej o równaniu: A.y=12x+212 B.y=−3x+1 C.y=−0,5x+2,5 D.y=−32+1 4.Punkt K dzieli bok AC trójkąta ABC w stosunku 2:5 licząc od punktu A. Punkt L leży na boku BC tak, że odcinek KL jest równoległy do boku AB. Odcinek KL ma długość 15, gdy: A.|AB|=21 B.|AB|=22 C.|AB|=52,5 D.|AB|=37,5 5.Okrąg o równaniu (x−2)2+(y+3)2=9: A.ma dwa punkty wspólne z prostą y=1 B. jest rozłączny z prostą x=1 C.jest styczny do osi odciętych D.jest styczny do osi rzędnych Prosiłbym o jakieś obliczenia lub sensowne tłumaczenie. Z góry dziękuję.

ogipierogi: 1. Można ze wzoru d=√c²+ab czyli d=√25+40=√65

Seba_xD: Czemy ab to 40 a c² 25 ? Skąd ta piątka ?

ogipierogi: 2. 2x=0 i x−5=0 x=0 i x=5 zaznaczasz na OX, parabola z ramionami w górę, kółka zamalowane, i zanaczasz sobie przedział gdzie ta funkcja jest ≤0 więc jest to obszar pod Osią Ox, należą do niej liczby z przedziału <0,5> − czyli 0,1,2,3,4,5 czyli w tym przedziale liczby pierwsze to 2,3,5 stąd odpowiedź a odpada. b również odpada bo parzyste jest 0,2,4 c jest prawidłowie bo są 3 nieparzyste − 1,3,5

ogipierogi: http://www.bazywiedzy.com/trapez-rownoramienny.php tu znajdziesz odpowiedź

Seba_xD: aa czaję, Dzięki za pomoc

Seba_xD: Pomoże ktoś przy pozostałych ?

Seba_xD: .