Prawdopodobieństwo Beata: W urnie znajduje się n kul białych i 2n kul czerwonych .Wybieramy losowo dwie kule. Dla jakich wartości n prawdopodobieństwo wylosowania kul o rożnych kolorach jest równe prawdopodobieństwu wybrania kul tego samego koloru?

Tad:

	3n 2		(3n)!		3n(3n−1)
|Ω|=		=		=
			2!*(3n−2)!		2

Jedną kulę białą z n białych możemy wylosować na n sposobów

	n 2		n!		n(n−1)
Dwie kule białe z n białych na ...		sposobów ....		=
			2!(n−2)!		2

Jedną kulę czarną z 2n czarnych możemy wylosować na 2n sposobów

	2n 2		(2n)!		2n(2n−1)
Dwie kule czarne z 2n czarnych ... na		sposobów ..		=
			2!(2n−2)!		2

... i chyba wszystko jasne −

Zrozpaczona : Jak dla mnie czarna magia Ale dziękuje Ci za pomoc

Tad: oczywiście

	n(n−1)		2n(2n−1)
n*2n=		+		.....n1=0 sprzeczny w war. zadania
	2		2

n₂=3

Tad: Obie czarne albo obie białe ..... suma Jedna czarna jedna biała .... iloczyn

Zrozpaczona : narazie dziura ale postaram sie to zrobić i spróbuje napisać moje rozwiązanie

Tad: ale czego tu nie rozumiesz?

Zrozpaczona : chwila bo zaczynam ogarniać

Zrozpaczona : a czemu n₂ wyszło 3?

Mila: Beato, czy umiesz rysować i odczytać prawdopodobieństwo z drzewka?

;(: Niestety wydaje mi sie ze to zadanie jest za bardzo skomplikowane jak na moje zdolności rysunku drzewka

Tad:

	n2−n+4n2−2n
2n2=
	2

Tad: 4n²=5n²−3n n²−3n=0 n(n−3)=0

;(: Tad właśnie miałam pisać czy dobrze to rozkminiłam ale mnie uprzedziłeś Jesteś wielki Masz u mnie piwo

Tad: − nie omieszkam się o nie upomnieć ... tylko już nie wiem kto stawia (Beata ... Zrozpaczona ...

;(: Dla Cb hmmm ? Dla Cb bedzie 3 w 1

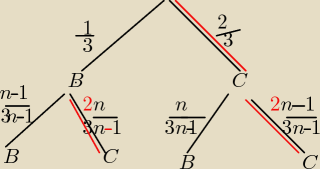
Mila: n+2n=3n

	1n		1
w I losowaniu Biała −z prawdopodobieństwem		=
	3n		3

	2n		2
Czerwona −z prawdopodobieństwem		=
	3n		3

II losowanie kul jest (3n−1)

	1		n−1
P(BB)=		*		mnożymy prawd. na gałązkach
	3		3n−1

	2		2n−1
P(CC)=		*
	3		3n−1

	1		2n
P(BC)=		*
	3		3n−1

	2		n
P(CB)=		*
	3		3n−1

P(BB)+P(CC)=P(BC)+P(CB)

1

n−1

2

2n−1

1

2n

2

n

*

+

*

=

*

+

*

3

3n−1

3

3n−1

3

3n−1

3

3n−1

Mianowniki są takie same , to n−1+2(2n−1)=2n+2n n=3

;(: Mila dla CB również piwko

Mila: