Strasznie pusto się zrobiła na forum na początku wakacji, choć parę osób jednak zagląda.
No to "pieczemy chlebek"
zad/ Udowodnij ,że długość średnicy okręgu wpisanego w trapez równoramienny
jest równa średniej geometrycznej długości podstaw tego trapezu.
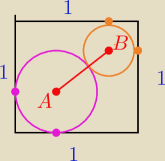Podaj długość odległości IABI
wiemy ,że bok kwadratu ma długość 1
a okręgi maja promienie r1 i r2
Podpowiem Odp: IABI = 2 − √2 
do zad. z okręgami: narysuj trójkat prostokątny
o przeciwprostokatnej IABI ....... i dalej już prosto
Dasz radę 
!
....
zad. z okręgami:
trójkąt prostokątny o przeciwprostokatnej IABI
ma przyprostokatne równej długości a = b = 1 − ( r1 +r2)
teraz zastosuj tw. Pitagorasa i policz IABI
dodatkowo IABI jest przekątną kwadratu o boku 1 − ( r1 +r2)
Policz i .... powinien wyjść ten wynik ,który podałam
tim − masz kwadrat o boku długości 1
Masz wpisane w niego 2 okręgi o promieniach r1 ≠ r2
Masz znaleźć odcinek łączący środki tych okręgów.
Podpowiedź: narysuj trójkąt prostokątny równoramienny wykorzystując odcinek AB 
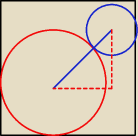Teraz jasne zadanie, to wiem
I już wcześniej zauważyłem, że przekątną trzeba poprowadzić (myślałem, że to 1/3 i 1/4),
więc:
Szukana długość |AB| = r1 + r2
r1 + r2 = √2(1 − r1 − r2)
r1 + r2 = √2 − √2r1 − √2r2
r1 + √2r1 + r2 + √2r2 = √2
(1 + √2)(r1 + r2) = √2
| √2 | ||
r1 + r2 = | ||
| 1 + √2 |
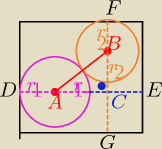IACI = IDEI − (IDAI + ICEI)
IACI= 1 − ( r1 + r2)
podobnie:
IBCI= IFGI − ( IFBI +ICGI)
IBCI= 1 − ( r2 +r1)
więc trójkat ABC jest prostokatnym i równoramiennym ( IACI=IBCI
więc IABI −−− długość przekatnej kwadratu o boku 1 −( r1 +r2)
zatem:
IABI= [1 −(r1+r2)]√2
ponad to IABI = r1 +r2 bo okręgi są styczne zewnętrznie
to:
IABI = √2 − IABI*√2
już teraz nie powiesz mi ,że nie policzysz IABI ?
.......pięknie
! .......łatwe
( dla Ciebie Timuś?..... pestka!)
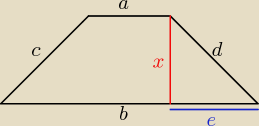Z założenia:
a + b = c + d
oraz c = d
| b − a | ||
oraz e = | ||
| 2 |
| a + b | ||
d = | ||
| 2 |
| b − a | a + b | |||
( | )2 + x2 = ( | )2 | ||
| 2 | 2 |
....... mniam, mniam....