Zadania Heksula: Czy ktoś może mi pomóc z tymi zadaniami? Zad. 4 Dany jest ostrosłup prawidłowy trójkątny o krawędziach bocznych dwa razy dłuższych od krawędzi podstawy. Oblicz tangens kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy. Zad. 5 Pole przekroju osiowego stożka jest równe pierwiastek z 3 cm, a kąt nachylenia tworzącej stożka do płaszczyzny podstawy ma miarę 60 stopni. Oblicz objętość i pole powierzchni bocznej tego stożka.

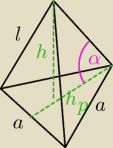
dero2005: l = 2a

	a√3
hp =
	2

	√33
h = √l2 − (23hp)2 = √(2a)2 − (23*a√32)2 = a
	3

	h
tg α =		= √11
	2   hp 3

Heksula: Dziękuję! A drugie zadanie ?

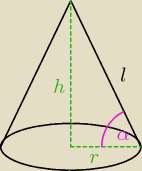
dero2005: α = 60^o r*h = √3

h
	= tg 60o = √3
r

h = √3 r = 1 l = √r² + h² =

	πr2
V =		=
	3

P_b = πrl =

dero2005:

	πr2*h
V =		=
	3

Heksula: Dziękuję! Zostało mi jeszcze jedno zadanie. Cenę lodówki podniesiono o 25%. O ile procent trzeba obniżyć nową cenę, aby lodówka kosztowała tyle samo co przed podwyżką?

dero2005: A − cena przed podwyżka p − obniżka

	A
p = 1 −		*100 [%]
	A*1,25

	1
p = (1 −		) * 100 = (1 − 0,8)*100 = 20%
	1,25