wykres funkcji Angela: Potrzebuję pomocy, mam takie zadanko sporządź wykres funkcji

	x−2
a) f(x)=
	x+1

	x2−2x−3
b) f(x)=
	x2−x−6

Proszę o pomoc

tim: 1. Wyznaczamy dziedzinę. 2. Skracamy jeżeli się da (patrz punkt b) ) 3. Robimy tabelkę i rysujemy wykres.

tim: Jeżeli jakiś problem − pisz, wytłumaczę

Angela: z tabelką problemu miec nie będę ani z wykresem Tylko to rozwiązanie − nie umiem

tim: Jakie rozwiązanie? Dobrze. Pokażę b), dobrze? 1. Rozkładamy na czynniki: x² − 2x − 3 = x² + x − 3x − 3 = x(x + 1) − 3(x + 1) = (x − 3)(x + 1) x² − x − 6 = x² + 2x − 3x − 6 = x(x + 2) − 3(x + 2) = (x − 3)(x + 2) Podstawiamy:

x2 − 2x − 3		(x − 3)(x + 1)		x + 1
	=		=
x2 − x − 6		(x − 3)(x + 2)		x + 2

Mamy skrócone, teraz dziedzina zał. x + 2 ≠ 0 x ≠ − 2 x ∊ R \ {−2} Tabelka + wykres (potrafisz )

Angela: czyli w tabelce y=x+2? czy to nie tak?

tim:

	x + 1
Nie. W tabelce cała skrócona funkcja:
	x + 2

Angela: nie kumam, jak?

tEa: Jeszcze zapiszemy tak: D_f= R \ { −2}

	x+1		x +2 −1		1
f(x) =		=		= 1 −
	x+2		x+2		x +2

wektor przesunięcia równoligłego funkcji g(x)

	−1
u= [−2, 1] g(x) =
	x

tim: Oj tam... Bez wektorów [Nie nawidzę ich ]

Angela: teraz to juz nic nie wiem z tego

Angela: proszę

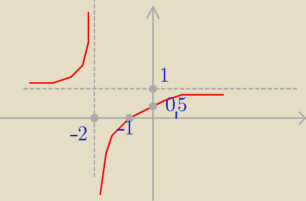
tim: Masz funkcję:

x + 1
x + 2

Podstawiasz okolo 5−10 roznych "x" (oprócz −2) i rysujesz , będzie to funkcjawymierna (hiperbola).

tEa:

Angela: ok dziekuję teraz będę próbować następne

tEa: powodzenia!

tim: Żeś herbatko namieszała

Angela: czyli co źle jest?

tEa: Co namieszałam? ...... chyba zamieszałam ? , by się cukier rozpuścił

tEa: Nie ..... jest OK My tak z Timusiem lubimy się .......

Angela: aha ok dziękuję

tEa:

tim: No dobra... Zamieszałaś Co za różnica, jedna literka xd

tEa: Ale..... różnica

tim: Zrobisz mi herbatkę, herbatko?

mit:

tEa: Właśnie piję ...... z rumem Ciekawe gdzie jest Basia? ..... smutno bez Niej

tEa: "mit" tak własnie miałam Ci napisać "imt" "mti"

tEa: A co na to? "danBog" Pozdrawiamy !

mit: donBag albo siaBa

tEa: ......mit Uns?

mit: Z rumem... ja też chce

mit: co?

tEa: siaBa ...... tak mówiła na swoje imię moja córka jak była malutka ( od Sabina)

mit:

tEa: z rumem? Nie masz 18− tu lat zabronione!

mit: <cry>

tEa:

mit: Oj tam... Jesczze niecałe 3 lata

mit: O co chodziło "mit Uns..?" − "z nami (po niemiecku? )

tEa: Dla Tima.... i innych ... Zad: Cyfrą jedności liczby trzycyfrowej jest 2 Jeżeli tę cyfrę przeniesiemy na początek tej liczby , to otrzymamy liczbę o 36 mniejszą od danej liczby. Jaka jest suma cyfr szukanej liczby?

Bogdan: Najwyraźniej się nudzicie

tEa: ......... tak , tak

mit: Heh Ale o co chodziło z mit Uns 100x + 10y − 34 = 200 + 10x + y 90x + 9y = 234 9(10x + y) = 234 10x + y = 26 x = 2 y = 6 z = 2 Suma cyfr: 2 + 6 + 2 = 10

tEa: Tim z Nami

mit: Ok

mit: Hot tEa ^.^

mit: A jak zmienimy | | albo b.?

tEa: Zad: Czy liczba nieparzysta i połowa liczby parzystej następującej bezpośrednio za nią mogą mieć wspólny dzielnik > 1 ? ( uzasadnić!)

mit: Oh. To nie ja

tEa: Eeeeeee tam ..... dasz radę na 100% Czekam na uzasadnienie.

mit: Niee.e...:(

tEa: No dobrze 2n +1 −−− liczba nieparzysta 2n+2 −−− następujaca po niej parzysta więc jej połowa jest postaci n +1 ponieważ 2n +1 = 2( n+1) −1 zatem 2( n+1) −1 i ( n+1) są względem siebie pierwsze. czyli nie moga mieć dzielnika > 1

mit: AaAaAaAaA

mit: Dlaczego są względem siebie pierwsze...? (nie rozumiem tego zdania)

tEa: Policzymy zatem z algorytmu Euklidesa:( znasz taki napewno) NWD(a,b)= NWD( a −b, b) NWD( 2n+1, n+1) = NWD( 2n+1 − n −1, n+1) = NWD( n, n+1)= NWD(n, n+1 −n)= NWD(n, 1) = 1 ....... więc są względem siebie pierwsze czyli nie mogą mieć dzielnika >1

mit: :( znasz taki napewno) −>> nie byłbym taki pewny na twoim miejscu

AS: 56 postów na tak proste zadania − czy nie przesada?

Squall: Przy jeszcze prostszych było 900 (przy tylu zniknąłem − miało być 1000)

tEa: