Na podstawie twierdzeń rachunku różniczkowego uzupełnij tabelę zmienności funkcj Ala: Na podstawie twierdzeń rachunku różniczkowego uzupełnij tabelę zmienności funkcji f: ____________________________________ |_x__ |₋ ∞↗ | 1 | ↗ | 3 | ↗ | 6 |_↗∞| | f' (x) | − | 0 | − | x | + | 0 | − | | f'' (x) | + | 0 | − | x | − | − | − | | f (x) | ∞ | 0 | −∞ | x | −∞ | −1 | −∞ | Wyznacz przedziały monotoniczności i ekstrema tej funkcji. wyznacz przedziały wypukłości i punkty przegięcia funkcji f. Wyznacz granice funkcji f na wszystkich jej krańcach jej przedziałów określoności. Naszkicuj wykres funkcji f.

AS: Co to jest x w tabeli?

Ala: na samej górze w rogu powinno być X / nie razy (x)

Ala: czy ktoś mi pomoże?

Ala: | x |− ∞↗ | 1 | ↗ | 3 | ↗ | 6 | ↗∞| | f' (x) | − | 0 | − | x | + | 0 | − | | f'' (x) | + | 0 | − | x | − | − | − | | f (x) | ∞ | 0 | −∞ | x | −∞ | −1 | −∞ |

AS: Ojej! Pytam się o x w kolumnie pod 3

Ala: to chyba oznacza brak

Ala: to nie bedzie asymptota pionowa w punkcie 3?

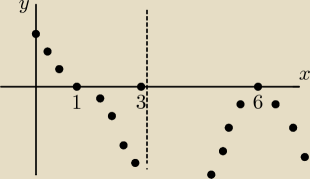
AS: Przedziały monotoniczności (−∞,3) maleje bo pierwsza pochodna ujemna w tym przedziale (3,6) rośnie bo pierwsza pochodna dodatnia w tym przedziale (6,∞) maleje bo pierwsza pochodna ujemna w tym przedziale Ekstrema w (6,0) maksimum bo pierwsza pochodna = 0 i zmienia znak z + na − z lewej strony (6,0) rośnie a z prawej maleje l;ub też drugie kryterium: f'(xo) = 0 , f''(xo) < 0 punkt przegięcia w (1,0) bo druga pochodna w tym punkcie przyjmuje wartość 0 Wypukła w (−∞,1) bo druga pochodna przyjmuje wartości dodatnie w każdym punkcie tego przedziału (styczna poprowadzona do krzywej w tym przedziale jest pod krzywą) Wklęsła w (1,3) oraz (3,∞ bo druga pochodna przyjmuje wartości ujemne w każdym punkcie tego przedziału (styczna poprowadzona do krzywej w tym przedziale jest nad krzywą) Granice: dla x → −∞ granicą jest +∞ dla x → 3− granicą jest −∞ (lewa strona 3 − granica lewostronna)) dla x → 3+ granicą jest −∞ (prawa strona 3 − granica prawostronna) dla x → ∞ granicą jest −∞ Wzorzec zapisu: lim f(x) = −∞ x→ ∞

Ala: Dziękuję, ślicznie

Ala: Jeszcze jedno pytanie ale czy funkcja nie powinna być w pkt (6,−1)

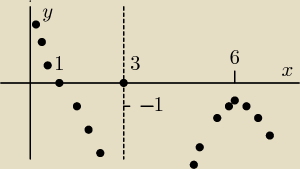
AS: Oczywiście że błąd ,przepraszam za pomyłkę Przedziały monotoniczności (−∞,3) maleje bo pierwsza pochodna ujemna w tym przedziale (3,6) rośnie bo pierwsza pochodna dodatnia w tym przedziale (6,∞) maleje bo pierwsza pochodna ujemna w tym przedziale Ekstrema w (6,−1) maksimum bo pierwsza pochodna = 0 i zmienia znak z + na − z lewej strony (6,−1) rośnie a z prawej maleje lub też drugie kryterium: f'(xo) = 0 , f''(xo) < 0 punkt przegięcia w (1,0) bo druga pochodna w tym punkcie przyjmuje wartość 0 Wypukła w (−∞,1) bo druga pochodna przyjmuje wartości dodatnie w każdym punkcie tego przedziału (styczna poprowadzona do krzywej w tym przedziale jest pod krzywą) Wklęsła w (1,3) oraz (3,∞) bo druga pochodna przyjmuje wartości ujemne w każdym punkcie tego przedziału (styczna poprowadzona do krzywej w tym przedziale jest nad krzywą) Granice: dla x → −∞ granicą jest +∞ dla x → 3− granicą jest −∞ (lewa strona 3 − granica lewostronna)) dla x → 3+ granicą jest −∞ (prawa strona 3 − granica prawostronna) dla x → ∞ granicą jest −∞ No teraz już chyba wszystko jest dobrze.

Ala: Dziękuję bardzo za taka stronę, uczyłam sie z niej przez pól roku na studiach, nigdy nie miałam problemu nawet maturę z matmy zdałam na 5 ale to było 18 lat temu. Rozwiazanie tego zadania pomogło mi bardzo zrozumieć kolejny materiał dziś miałam wpis do indeksu i otrzymałam 5. Zadanie miałam wprawdzie trudniesze ale poradzilam sobie dziękuję raz jeszcze

AS: Dziękuję i ja za informację,trochę satysfakcji i dla mnie.