Badanie funkcji Krzysiek: Słuchajcie, nie rozumiem do końca polecenia: "znajdź przedział, w którym funkcja jest rosnąca i wypukła w górę." Mam znaleźć przedziały gdzie odpowiednio funkcja jest rosnąca i wypukła w górę, a potem wyciągnąć z nich część wspólną? Czy policzyć (dla tego przypadku) gdzie f`(x)>0 i f``(x)<0 w następujący sposób:

	ex
f(x)=		, Df(x)= R\{−1}
	x+1

	xex
f`(x)=		, Df`{(x)}= Df(x)
	(x+1)2

xex
	>0
(x+1)2

xe^x(x+1)²>0 stąd miejsca zerowe to: x= 0, x= −1 odpada, bo nie jest w dziedzinie, no i co z tym e^x?

Krzysiek: Dobra, lecimy dalej: xe^x(x+1)²>0 x>0, bo (x+1) i e^x niczego nie wnoszą do obliczeń ze względu na to, że e^x>0 dla x∊R, a x≠−1 Stąd f(x) jest rosnące dla x>0

	ex−xex
f``(x)=		, żeby f(x) była wypukła w górę⇒ f``(x)<0
	(1+x)3

D_f``(x)= D_f(x) e^x(1−x)(1+x)³<0 1−x<0 1<x stąd f(x) wypukła w górę dla x>1 Zatem f(x) wypukła w górę i rosnąca dla x∊(1,+inf) Może mi ktoś to sprawdzić?

Vizer: Hmm czyli dla x = −2 funkcja nie będzie wklęsła ?

Krzysiek: http://www.wolframalpha.com/input/?i=f%28x%29%3D-e%5E%28-2%29

Vizer: Eh może się źle wyraziłem. Po prostu zgubiłeś rozwiązania : e^x(x − 1)(x + 1)³ > 0 x ∊ (− ∞, −1) U (1 , +∞)

Krzysiek: zauważyłem, że zrobiłem błąd: (1−x)(1+x)³<0 (1+x)³ ma nieokreślony znak więc może wpływać na nierówność. Nie wiem jednak jak to rozwiązać...

Vizer: Ale co nie wiesz ? Jak rozwiązać nierówności, czy co ?

Krzysiek: Tak. Jak rozwiązać tą nierówność.

Vizer: No to rozwiązałem wyżej, czy widzisz, ale nie rozumiesz wyniku ?

Krzysiek: e^x można wywalić, bo zawsze >0, ale co z tym (x+1)³?

Vizer: To wystarczy teraz rozwiązać taka nierówność : (x − 1)(x + 1) ³ > 0 Pamiętasz w liceum jak to się robiło ?

Krzysiek: Siedzę nad tą matmą prawie 7 godzin. Już mi się wszystko pie*doli. Zlituj się, proszę.

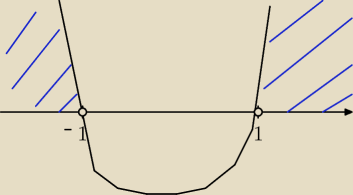
Vizer: Jest to wielomian 4 stopnia a dodatnim współczynniku, więc rysujemy wykres od lewej "od góry do góry"

Krzysiek: HAHAHAHAHAHAHAHHAHAHAHA! Chyba dość na dzisiaj...

	ex
Dobra, mam w takim razie przedział (−1,1), w którym to funkcja f(x)=		jest wypukła w
	x+1

górę. Mam też przedział x>0, w którym f(x) jest rosnąca. Zatem funkcja jest rosnąca i wypukła w górę na przedziale (0,1), dobrze?

Vizer: Tak

Krzysiek: Hurra! Pomógłbyś mi jeszcze ze znalezieniem punktu przegięcia? Liczę drugą pochodną f(x)= e^cosx f`(x)= e^cosx*(−sinx) f``(x)= −cosx*e^cosx−sinx*e^cosx*(−sinx)= −cosxe^cosx+sin²xe^cosx= e^cosx(sin²x−cosx)= e^cosx(1−cos²x−cosx) e^cosx(1−cos²x−cosx)= 0 cos²x+cosx= 1 cosx(cosx+1)= 1 cosx= 1 u cosx= 0 cosx= 1 dla 2kπ

	π
cosx= 0 dla		+kπ
	2

f``(x<sub>0</sub>)= 0⇒ f``(2π)= e¹(1−1−1)= −e≠0

	π
f``(x0)= 0⇒ f``(		)= e0(1−0−0)= 1≠0
	2

Coś na bank robię źle.

Vizer: cosx(cosx + 1) = 1 cosx = 1 v cosx = 0 Tu jest źle, pewnie pomyliłeś sobie z równością z zerem, bo tak się robi gdy przyrównujemy iloczyn do 0. Tutaj należy wszystko na jedną stronę przenieść i wyliczyć bez kombinacji równanie kwadratowe.

Krzysiek:

	−1+√5
w takim razie cosx=
	2

	−1−√5
cosx=
	2

I co dalej? Jak mam sprawdzić, czy druga pochodna jest równa 0?

Krzysiek:

	−1−√5
cosx=		odpada, bo jest większe od −1, a to jest nie możliwe.
	2

Vizer: Tak widzę, że wyniki ładne nie wyszły, albo z tablic jakieś przybliżone wartosci albo zapisać, że

	−1 + √5
x = arccos(		)
	2

Krzysiek: Hmm, widzę zależność, że np. tgx= a⇒ x= arctg(a). Przyda się. No to lipa. Jutro poprawa egzaminu. Ostatnia szansa Trafiłem bardzo, bardzo źle z ćwiczeniowcem... Dzięki za pomoc. Miłego wieczoru.