geometria analityczna Łukasz: Dane są dwa kolejne wierzchołki równoległoboku ABCD: A(−2,−1) i B(6,3). Wiedząc że przekątne tego równoległoboku przecinają się w punkcie E (1,3). a) wyznacz współrzędne wierzchołków C, D b) wykaż że równoległobok ABCD jest prostokątem.

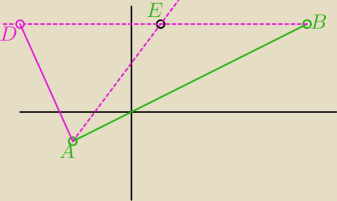
Skipper: Punkt przecięcia się przekątnych dzieli je na równe części Punkty B, E a więc i D leżą na prostej y=3 Liczymy |BE|=5 Na prostej y=3 szukamy punktu D takiego, że |DE|=5 D (−4;3)

	3+1
Prosta zawierająca odcinek AB m: y−3=		(x−6)
	6+2

	1
m: y=		x
	2

	3+1
Prosta zawierająca odcinek AD n: y−3=		(x+4)
	−4+2

n: y=−2x−5 ... i widać, że proste m i n są prostopadłe Punkt C ... to już banał−