dla jakich wartosci parametru a równanie ma nieskonczenie wiele rozwiazan
ed: dla jakich wartosci parametru a równanie ma nieskonczenie wiele rozwiazan
|x|+|x−1|=a
6 lut 16:44
ed: 
6 lut 16:53
Mila: Rozwiąż graficznie.
6 lut 16:58
ed: a da się algebraicznie?
6 lut 17:07
ed: ?
6 lut 17:17
Mila:
|x|=x dla x≥0
|x−1|=x−1 dla x≥1
1) x<0
|x|=−x ; |x−1|=−x+1
−x−x+1=a
−2x=a−1
| | −a+1 | |
x= |
| jedno rozwiązanie |
| | 2 | |
2)x∊<0;1)
|x|=x ; |x−1|=−x+1
x−x+1=a
0x+1=a
dla a=1 nieskończenie wiele rozwiązań
dla a≠1 brak rozwiązań
3) x≥1
x+x−1=a jedno rozwiązanie
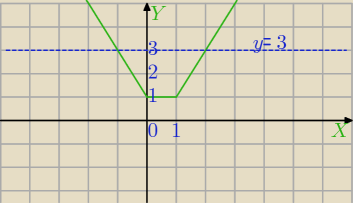
Graficznie
f(x)=−2x+1 dla x<0
f(x)=1 dla x∊<0;1)
f(x)=2x−1 dla x>1
y=a prosta pozioma , dla a=1 ma nieskończenie wiele punktów wspólnych z wykresem.
6 lut 18:13

 |x|=x dla x≥0
|x−1|=x−1 dla x≥1
1) x<0
|x|=−x ; |x−1|=−x+1
−x−x+1=a
−2x=a−1
|x|=x dla x≥0
|x−1|=x−1 dla x≥1
1) x<0
|x|=−x ; |x−1|=−x+1
−x−x+1=a
−2x=a−1