.
asdf: 
dobierz argumenty tak, aby funkcja była ciągła w pkt x
0 = 0
| | ln(1−x) | |
f(x) = { |
| , x < 0 |
| | ax | |
{ bx + 1, x ≥ 0
liczę granicę dla pierwszego (bez limesów):
| ln(1+ (−x)) | | ln(1+(−x)) * −1 | | −1 | |
| = |
| = |
| |
| ax | | −x * a | | a | |
| | −1 | |
dla drugiego mam granicę równą 1? czyli |
| musi być równe 1, więc mam: |
| | a | |
b = 0
pewnie źle..pierwszy raz to robię
5 lut 23:43
Trivial:
f(0
−) = f(0
+) = f(0)
a = −1.
b dowolne.
5 lut 23:46
asdf: e to proste..
dzieki
5 lut 23:49
asdf: czyli dobrze robiłem, teraz drugie pytanie: jak polubić macierze?
5 lut 23:50
asdf: jak wyznaczyć równanie styczne i normalne dla wykresy funkcji f(x)= xarctgx w pktcie x0 =
0?
5 lut 23:50
Trivial:
Równanie stycznej...
y = ax + b
a = f'(x0) ← geometryczna interpretacja pochodnej.
y0 = f(x0)
Dla punktu x0 zachodzi
y0 = ax0 + b
b = y0 − f'(x0)*x0
Podstawiamy do równania
y = f'(x0)*x + y0 − f'(x0)*x0
Równanie stycznej to:
y−y0 = f'(x0)*(x−x0)
5 lut 23:57
Trivial: Tyle że pochodna w punkcie x0 = 0 nie istnieje...
6 lut 00:03
asdf: ok dzieki
6 lut 00:09
asdf: a jak to zrobić:
limn−>oo n√e + cos2n{sgn(n−3)}
ograniczam to przez cos2n tak? a co z signum? opuszczam bez znaku − bo wartości dążą do inf?
6 lut 00:12
Trivial:
Dla n > 3 mamy:
1 ← n√e−1 ≤ n√e+cos2n{sgn(n−3)} ≤ n√e+1 → 1
↓
1
6 lut 00:24
asdf: a ten signum jak działa?
6 lut 00:25
Trivial:
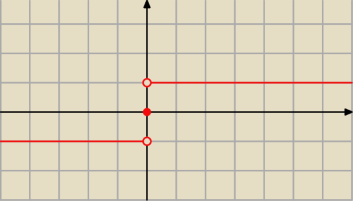
6 lut 00:28
asdf: ok, to takie |x|/x?
6 lut 00:28
Michał Anioł: dokładnie tak, tylko że do tego została zdefiniowana wartość w 0 jako 0
6 lut 00:33
Trivial:
To po prostu znak liczby.
Jeśli + to 1
Jeśli − to −1
Jeśli 0 to 0.
6 lut 00:33
asdf: dzięki
6 lut 00:40