wykaż że
szymek: W trójkącie prostokątnym ABC, w którym kąt przy wierzchołku C jest kątem prostym, poprowadzono
środkowe AD i BE. Udowodnij, że 4(AD2+ BE2)= 5 AB2
5 lut 23:24
Eta:
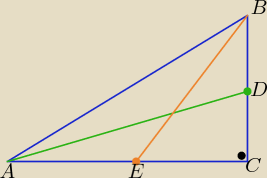
Dwa razy z tw. Pitagorasa
| | 1 | |
|AD|2= |AC|2+ |DC|2 = |AC|2+ |
| |BC|2 /*4 |
| | 4 | |
| | 1 | |
|BE|2= |BC|2+ |EC|2= |BC|2+ |
| |EC|2 /*4 |
| | 4 | |
dodajemy stronami:
4(|AD|
2|+|BE|
2)= 5(|AC|
2+|BC|
2) = 5|AB|
2
c.n.u
5 lut 23:35
Mila:
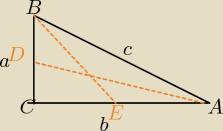
zał.
ΔACB− Δprostokątny
|CE|=|EA|
|CD|=|DB|
4(AD
2+BE
2)=5AB
2
Dowód
wΔACD:
| | 1 | | 1 | |
|AD|2=b2+( |
| a)2=b2+ |
| a2 z tw. Pitagorasa |
| | 2 | | 4 | |
W ΔBCE: z tw. Pitagorasa
| | 1 | | 1 | |
|BE|2=a2+( |
| b)2=a2+ |
| b2 |
| | 2 | | 4 | |
|AB|
2=a
2+b
2 z tw. Pitagorasa w ΔACB
5|AB|
2=5a
2+5b
2
4|AD|
2=4b
2+a
2
4|BE|
2=4a
2+b
2
4(AD
2+BE
2)=4b
2+a
2+4a
2+b
2=5a
2+5b
2=5|AB|
2
cnw
5 lut 23:39
Skipper:
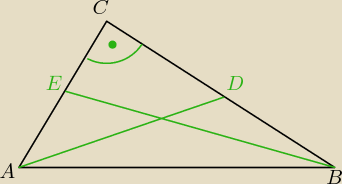
z cóż tu udowadniać −

Pobaw się Pitagorasem
5 lut 23:42
Eta:

5 lut 23:44
 Dwa razy z tw. Pitagorasa
Dwa razy z tw. Pitagorasa
 zał.
ΔACB− Δprostokątny
|CE|=|EA|
|CD|=|DB|
4(AD2+BE2)=5AB2
Dowód
wΔACD:
zał.
ΔACB− Δprostokątny
|CE|=|EA|
|CD|=|DB|
4(AD2+BE2)=5AB2
Dowód
wΔACD:
 z cóż tu udowadniać −
z cóż tu udowadniać − Pobaw się Pitagorasem
Pobaw się Pitagorasem
