? Patryk: dla jakich wartości parametru m pierwiastki równania x²−2mx−m−2=0 są zawarte miedzy liczbami −2 i 4 ? f(4)<0 f(−2)<0 Δ>0 −2<X_w<4 tak ?

Dominik: f(−2) > 0 f(4) > 0 reszta ok

Kamcio :): Moim zdaniem delta nie musi być rózna od 0

Dominik: musi. dla Δ = 0 mamy jeden pierwiastek PODWOJNY, a w tresci jest mowa o pierwiastkach.

Patryk: 5 lut 2013 21:26 dlaczego tak ?

Dominik: bo a > 0. naszkicuj sobie funkcje z moimi i twoimi zalozeniami.

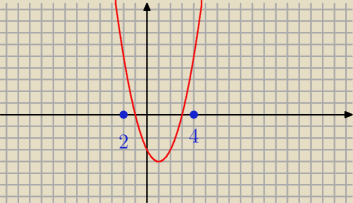
Nienor: Myślę, że ten rysunek wiele wyjaśnia.

Patryk: teraz rozumiem,dzieki

Madzia: po prostu trzeba sobie napisać 4>x₁>−2 a drugie 4>x₂>−2 x₁ i x₂ policzyć normalnie z delty i rozwiązać te dwa równania

Madzia: nie trzeba rysunku

Dominik: no chyba nie

Madzia: i oczywiście żeby były pierwiastki to delta więkasz od 0

Patryk: (x1<4∧x1>−2)∨(x2<4∧x2>−2) to tak ?

Dominik: wszedzie koniunkcja, a nie alternatywa. ale nie rozumiem − PO CO? wczesniej miales proste zalozenia, ktore latwo sie liczylo.

Madzia: Δ>0 => Δ=4 x₁=m−1 m−1<4 m−1>−2 z tego : m ∊(−1:5) x₂=m+1 m+1<4 m+1>−2 z tego m∊(−3:3) odp: m∊(−1:3)

Nienor: Δ=4m²+4(m+2)=4m²+4m+8 √Δ=√4m²+4m+8

	2m±√4m2+4m+8
x=
	2

Tak, zdecydowania lepiej rozwiązać 4 tak piękne równania, niż narysować sobie i trochę pomyśleć.

Dominik: @Madzia, skad to?

Nienor: Δ>0 ⇔ m=4 4m²+4m+8>0 ⇔ m²+m+2>0 Δ=1−4*2=−7 m∊R

Dominik: chyba najlepiej taka pomoc zignorowac.

Madzia: moje to do takiego samego zadania tylko o równaniu x²−2mx+m²−1=0 ale o to samo chodzi

Nienor: Racja, tylko twoje równania jest wyjątkowe, metoda tu zastosowana nijak się ma do równania Patryka

jikA: Nie rozumiem o co chodzi Madzia równanie jest napisane powyżej a Ty robisz zupełnie inne?

Madzia: ok

Nienor: Chyba uważa, że jeden trik można stosować zawsze, ale to przeczy przecież definicji triku

Dominik: w zasadzie jakby sie uprzec to mozna to tak liczyc − rownania wcale nie sa az tak paskudne. trikiem natomiast sa zalozenia typu x_w, f(2)> 0 etc.

Nienor: Można, można, jako truk mi chodzi, że Δ nie zależy od parametru A to z f(−2)>0 jest raczej metodą, obok oczywiście wylicznia pierwiastków i podstawiania do równania.