zastosowanie calek damiano120: Witam, mam pewien problem z zdaniami z zastosowania calek. Czy moglby mi ktos jasno, obrazowo obliczyc te zadania, tak zebym mogl to zrozumiec: Obliczyc pola figur wewnatrz nastepujacych krzywych: r=√cos3x r=2sin3x r=2 / 2+cosx dla przedzialu od 0 do 2pi oczywiscie x jest to kąt, ale nie wiem jak sie wstawia znak "fi" Z góry dzieki i pozdrawiam.

AS: Czy mam rozumieć że to są równania w postaci biegunowej. (r?)

damiano120: Tak. Sa to rownania w postaci biegunowej. A wzor to: 1/2 calki r² (x) dx x−>fi oczywiscie calka jest ograniczona wyzej wymienionym przedzialem 0 ; 2pi

AS: Ok

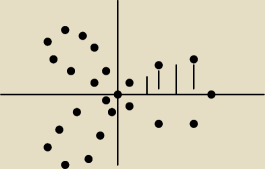
AS: Figura składa się z trzech pętli przystających lub 6 połówek tych pętli. Wystarczy wyliczyć jedną taką część a potem pomnożyć przez 6 by uzyskać wynik Kąt 3*fi zmienia się w zakresie 0 − π/2,a sam kąt fi w zakresie 0 − π/6 Wzór funkcji r = √cos(3*fi) Znak | zastępować będzie znak całki π/6 1 π/6 1 sin(3*fi) | π/6 P1 = 0.5|r²dfi = −− * |cos(3*fi)dfi = −− −−−−−− | 0 2 0 2 3 0 P1 = 1/6*(sin(3*π/6) − sin(3*0)) = 1/6*(sin(π/2) − sin(0)) = 1/6*1 = 1/6 Pole całej figury (6 pętli) P = 6*1/6 = 1

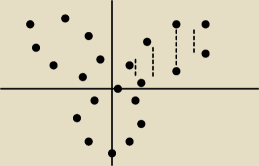
AS: Krzywa składa się z trzech pętli przystających. Wystarczy wyliczyć pole jednej pętli a potem pomnożyć przez 3 Pierwsza pętla (zakreskowana) zaczyna się w początku układu i w nim kończy. Tym samym kąt 3*fi zmienia się w zakresie (0 − 180) (sin(0) = 0 dla początku i sin (180^o) = 0 dla końca) Kąt fi zmieniać się będzie w zakresie (0 − π/3) − granice całkowania Równanie funkcji: r = 2*sin(3*fi) 1 π/3 1 π/3 π/3 P1 = −− |r²dfi = −− |4*sin²(3*fi)dfi = 2|(1 − cos(6*fi)/2 dfi 2 0 2 0 0 Wykorzystałem tożsamość trygonometryczną: sin²x = (1 − cos(2*x))/2 π/3 P1 = (fi − 1/6*sin(6*fi)) | = π/3 − 1/6*sin(6*π/3) − 0 + 1/6*sin(6*0) = P1 = π/3 − 1/6*sin(2*π) = π/3 − 0 = π/3 Pole całej figury: P = 3*P1 = 3*π/3 = π 0

AS: Uwaga: 0 uciekło spod całki w 3−im wierszu od dołu.

damiano120: Wielkie dzieki AS za jasne i profesionalne przedstawienie zadan Juz siadam, analizuje i mam nadzieje, że nie bede glupszy niż jestem Dzieki i pozdrawiam.

AS: Zachęciłeś mnie do rozwiązania zadania trzeciego. Jest bardzo trudne. Ale spróbuję. Z całkami już dawno się pożegnałem i muszę sobie wiele rzeczy przypominać. Pozdrowienia.

AS: Wyliczam całkę nieoznaczoną ( | oznaczam jako całka) 2 r = −−−−−−−−−−−− 2 + cosf Podstawienie: tg(f/2) = t => f = 2*arctgt cos²(f/2) – sin²(f/2) po podzieleniu licznika i mianownika cosf = −−−−−−−−−−−−−−−− przez cos²(f/2) cos²(f/2) + sin²(f/2) 1 – tg²(f/2) 1 – t² cosf = −−−−−−−−−− = −−−−−−− cosf wyrażone przez t 1 + tg²(f/2) 1 + t² Obliczam różniczkę dt df = f’*dt = 2* −−−−− 1 + t² 4 df J = 1/2*|r²*df = 1/2*| −−−−−−− df = 2*| −−−−−−−−− (2 + cosf)² (2 + cosf)² 2* dt −−−−−−−−−− 1 + t² dt (1 + t²)² J = 2* | −−−−−−−−−−−−− = 4*| −−−−− * −−−−−−−−−−−−−− 1 – t² 1 + t² (2 + 2*t² + 1 – t²)² (2 + −−−−− )² 1 + t² 1 + t² 3 + t² − 2 1 dt 2dt J = 4*| −−−−−−−−−dt = 4*| −−−−−−− = 4*( | −−−−−− − | −−−−−−− ) (3 + t²)² (3 + t²)² 3 + t² (3 + t²)² dt dt J = 4| −−−−−− − 8| −−−−−−−− = 4*J1 – 8*J2 3 + t² (3 + t²)² dt J1 = |−−−−−−−−− Stosuję podstawienie t = V3 *z dt = V3*dz 3 + t² V3 dz V3 dz V3 V3 J1 = | −−−−−−−−−− = −−− | −−−−−−−− = −−− *arctg(z) = −−*arctg(t/V3) 3 + (V3*z)² 3 1 + z² 3 3 dt J2 = |−−−−−−−− Podstawiam t = V3*z dt = V3dz (3 + t²)² V3dz V3 dz V3 z² + 1 − z² J2 = |−−−−−−−− = −−− |−−−−−−−− = −−− | −−−−−−−−−−dz = (3 + 3z²)² 9 (1 + z²)² 9 (1 + z²)² V3 dz z² V3 = −−− (|−−−−−−−− − | −−−−−−− dz) = −−− (arctgz − J3) 9 1 + z² (1 + z²)² 9 J3 = |z²dz/(1 + z²)² = |z*zdz/(1 + z²)² całkuję przez części u = z dv = zdz/(1 + z²)² du = dz v = |zdz/(1 + z²)² podstawiam 1 + z² = t 2zdz = dt ⇒ zdz = dt/2 v = 1/2*|dt/t²dt = 1/2*|t⁽−2)dt = −1/(2*t) = −1/2*(1 + z²) |udv = u*v − v|du J3 = z*(−1/(1 + z²)²) − 1/2|−1dz/(1 + z²) = −z/(1 + z²) + 1/2|dz/(1 + z²) J3 = −z/(1 + z²) + 1/2arctgz Podstawiając z = t/V3 otrzymamy J3 = −t/V3/(1 + t²/3) + arctg(t/V3) = −tV3/(3 + t³) = arctg(t/V3) J2 = V3/9(arctg(t/V3) + tV3/(3 + t²) − arctg(t/V3) J = 4*J1 − 8*J2 Tyle wymęczyłem − na więcej nie mam sił i czasu. Mam nadzieję że nie popełniłem błędu

damiano120: Troche spoznione ale dzieki bardzo AS troche sie nameczyles przy tym ale m.in dzieki Tobie zaliczylem egzamin z matematyki