ciekawe Madzia: Proszę o pomoc w ogóle nie mam pomysłu W ostrosłupie prawidłowym czworokątnym wpisano stożek. a) znajdź objętość ostrosłupa i objętość stożka, wiedząc że krawędź podstawy ostrosłupa ma długość α, natomiast tworząca stożka jest nachylona do podstawy pod kątem o mierze α. b) oblicz stosunek pola powierzchni bocznej stożka i ostrosłupa.

Madzia: ?

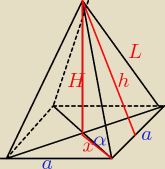
Basia: podstawą ostrosłupa jest kwadrat do policzenia objętości jest Ci potrzebne H x to połowa przekątnej kwadratu d² = a²+a² d² = 2a² d = a√2

	a√2
x =
	2

	H
tgα =
	x

	a√2*tgα
H = x*tgα =
	2

podstaw do wzoru na objętość i policz podstawą stożka jest koło wpisane w kwadrat więc r=^a₂ wysokość jest ta sama −−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	L
cosα=
	x

L = x*cosα

	a√2cosα
L =
	2

wylicz h z tw.Pitagorasa h to wysokość ściany bocznej i równocześnie tworząca srożka P_bo = 4*¹₂a*h P_bs = πrh

Basia: właściwie to h nie jest Ci potrzebne, bo masz policzyć tylko

Pbs		πrh		πr		πa2		π
	=		=		=		=
Pbo		2ah		2a		2a		4

Madzia: w odp mam v=(a³ tgα)/ 6 a jeśli a mi dodatkowo wychodzi √2 w liczniku

Basia: dobrze Ci wychodzi, nie wiem gdzie oni go zgubili

Madzia: ok to i tak dziękuje

Madzia: już wiem gdzie jest błąd nie bierzemy pod uwagę połowy przekątnej tylko połowę boku podstawy bo to jest nachylona tworząca do podstawy a to jest (1/2)a wyjdzie wtedy do pierwiastka