.
qwerty: Jak naszkicować wykres tej funkcji
f(x)= |x| − |x−1|
5 lut 15:08
Artur_z_miasta_Neptuna:
podziel na 3 przedziały ... wyznacz postac funkcji dla każdego z tych przedziałów
5 lut 15:09
qwerty: x>0 i x∊<0,1) i x∊<1,
∞) takie


5 lut 15:12
Basia: takie

5 lut 15:13
Artur_z_miasta_Neptuna:
si
5 lut 15:13
Dominik: mialy byc 3 przedzialy − ja tu widze dwa.
I x∊(−∞, 0)
II x∊<0, 1)
III x∊<1, ∞)
5 lut 15:14
qwerty: tak masz racje w pierwszym miało być x<0

5 lut 15:16
Dominik: to sie zgadza.

5 lut 15:18
qwerty: jeszcze takie pytanko jak mam ukałd równań
| ⎧ | 2|x|+y=0 | |
| ⎩ | x−|y|=−1 | to na jakich przedziałach to zrobić?
|
5 lut 15:19
Dominik: x ≥ 0, y ≥ 0
x ≥ 0, y < 0
x < 0, y ≥ 0
x < 0, y < 0
5 lut 15:20
Dominik: wszystko z def wartosci bezwzglednej
5 lut 15:20
Basia: tu trudno mówić o przedziałach
rozważ 4 przypadki
1. x≥0 i y≥0
2. x≥0 i y<0
3. x<0 i y≥0
4. x<0 i y<0
5 lut 15:21
qwerty: albo np
| ⎧ | |x| + |y| = 4 | |
| ⎩ | 4|x| − y = 1 |
|
?
5 lut 15:21
Basia: tak samo jak poprzednio
5 lut 15:22
qwerty: nie potrafie sam wyznaczyć tych przedziałów...
5 lut 15:26
Basia:
jakich przedziałów ?
rozpatrujesz te cztery przypadki
1.
x≥0 i y≥0
masz wtedy układ
x+y=4
4x−y = 1
−−−−−−−−−−−−−−−−−
5x = 5
x=1
y=3
jest jedno rozwiązanie : x=1 y=3
2.
x≥0 i y<0
wtedy masz
x−y = 4
4x−y = 1
−x+y = −4
4x−y = 1
−−−−−−−−−−−−−−−
3x = −3
x= −1
odpada bo miało być x≥0
w tym przypadku nie ma rozwiązania
tak samo zrób przypadki 3 i 4
5 lut 15:42
qwerty: chodzi mi o to, że jakoś źle układam te "przypadki"
5 lut 17:31
Basia:
3. x<0 i y≥0
4. x<0 i y<0
te przypadki zależą od tego co jest "wewnątrz" wartości bezwzględnej
raczej nie da się tego jakoś ogólnie opisać
5 lut 17:33
Mila:
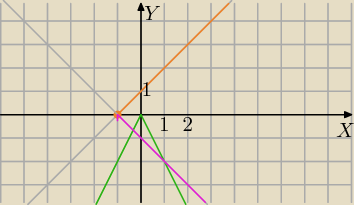
Ja mam taki sposób: (graficznie i spr. algebraiczne)
2|x|+y=0
x−|y|=−1
1) y=−2|x| wykres zielony
2) |y|=x+1
Tu rozpatruję 2 przypadki
a) y≥0 ( nad osią OX)
y=x+1 pomarańczowy wykres
b) y<0 (pod osią OX
|y|=−y
−y=x+1 ⇔y=−x−1 różowy wykres
są dwa punkty przecięcia ; jeden dokładny
x=1 i y=−2
drugi trzeba obliczyć
różowa "gałązka" ma wzór y=−x−1
zielona lewa y=2x
| | −1 | | −2 | |
2x=−x−1 ⇔3x=−1 ⇔x= |
| to y= |
| |
| | 3 | | 3 | |
teraz pozostaje Ci wstawić do początkowego układu i sprawdzić.
5 lut 17:50
qwerty: ogólnie mi chodzi nie tylko o 3 i 4..
5 lut 17:50
Mart: jeśli chodzi o funkcje to latwiej narysować sobie przedzialy no ... wyznacza sie miejsca zerowe
wart. bezw. zaznacza je na osi i po kolei leci sie przedzialami ...
5 lut 17:51
Mila:
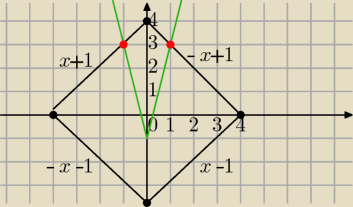
Metoda graficzna
|x| + |y| = 4
4|x| − y = 1
1) |x| + |y| = 4
takie równanie ma wykres w postaci jak na rysunku (zapamiętaj, bo szkoda czasu na kilka
przypadków, możesz to zrobić jeden raz)
(
czarny)
2) y=4|x|−1 zielony
masz dwa dokładne punkty, sprawdź albo ułóż równania
5 lut 18:03
Basia:
a jak to będzie układ
|x|+2|y| = √5
12x − 5|y| = √7
to też metoda graficzna się sprawdzi ?
bardzo wątpię
5 lut 18:07
Mat: że niby problem w √5 /? eeetam
5 lut 18:19
Basia: nie; raczej problem w 2|y|
5 lut 18:20
Mila:
Nie ma metody jedynie słusznej.
Wybiera się najprostszą w danym przypadku.
Każdy musi znaleźć sam swoją ścieżkę do wiedzy.
Pozdrawiam.

5 lut 18:26





 Ja mam taki sposób: (graficznie i spr. algebraiczne)
2|x|+y=0
x−|y|=−1
1) y=−2|x| wykres zielony
2) |y|=x+1
Tu rozpatruję 2 przypadki
a) y≥0 ( nad osią OX)
y=x+1 pomarańczowy wykres
b) y<0 (pod osią OX
|y|=−y
−y=x+1 ⇔y=−x−1 różowy wykres
są dwa punkty przecięcia ; jeden dokładny
x=1 i y=−2
drugi trzeba obliczyć
różowa "gałązka" ma wzór y=−x−1
zielona lewa y=2x
Ja mam taki sposób: (graficznie i spr. algebraiczne)
2|x|+y=0
x−|y|=−1
1) y=−2|x| wykres zielony
2) |y|=x+1
Tu rozpatruję 2 przypadki
a) y≥0 ( nad osią OX)
y=x+1 pomarańczowy wykres
b) y<0 (pod osią OX
|y|=−y
−y=x+1 ⇔y=−x−1 różowy wykres
są dwa punkty przecięcia ; jeden dokładny
x=1 i y=−2
drugi trzeba obliczyć
różowa "gałązka" ma wzór y=−x−1
zielona lewa y=2x
 Metoda graficzna
|x| + |y| = 4
4|x| − y = 1
1) |x| + |y| = 4
takie równanie ma wykres w postaci jak na rysunku (zapamiętaj, bo szkoda czasu na kilka
przypadków, możesz to zrobić jeden raz)
(czarny)
2) y=4|x|−1 zielony
masz dwa dokładne punkty, sprawdź albo ułóż równania
Metoda graficzna
|x| + |y| = 4
4|x| − y = 1
1) |x| + |y| = 4
takie równanie ma wykres w postaci jak na rysunku (zapamiętaj, bo szkoda czasu na kilka
przypadków, możesz to zrobić jeden raz)
(czarny)
2) y=4|x|−1 zielony
masz dwa dokładne punkty, sprawdź albo ułóż równania
