
 ŚKM−owskie zadanie z dzisiaj; etap rejonowy:
4/ X ŚKM − II − 5.01.2013
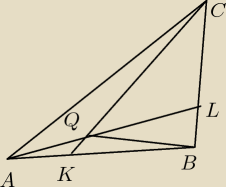
Na boku AB trójkąta ABC obrano taki punkt K, że KB=3*AK, a na boku BC tego trójkąta obrano taki
punkt L, że CL=3*BL. Niech Q będzie punktem przecięcia prostych AL i CK. Znajdź stosunek pola
trójkąta BQC do pola trójkąta ABC.
ŚKM−owskie zadanie z dzisiaj; etap rejonowy:
4/ X ŚKM − II − 5.01.2013
Na boku AB trójkąta ABC obrano taki punkt K, że KB=3*AK, a na boku BC tego trójkąta obrano taki
punkt L, że CL=3*BL. Niech Q będzie punktem przecięcia prostych AL i CK. Znajdź stosunek pola
trójkąta BQC do pola trójkąta ABC.
| 3 | 2 | 9 | ||||
Mi szczerze mówiąc wyszło | , ale słyszałem też coś o | , | ... | |||
| 4 | 3 | 13 |
| 9 | ||
Poprawna jest odpowiedź | . | |
| 13 |
| 1 | ||
Jeżeli oznaczyć symbolem S szukane pole trójkąta BQC, to pole trójkąta BLQ jest równe | S | |
| 4 |
| 3 | ||
(1) S+3T= | P | |
| 4 |
| 1 | 1 | |||
(2) | S+4T= | P | ||
| 4 | 4 |
| 3 | ||
trójkąt KBC ma podstawę równą | podstawy trójkąta ABC, a trójkąt BLA ma podstawę równą | |
| 4 |
| 1 | ||
podstawy trójkąta BCA. | ||
| 4 |
| 9 | ||
Rozwiązanie układy równań (1) i (2) daje odpowiedź S= | . | |
| 13 |