help :)
Wydi: 1.)Przekrój osiowy walca ma obwód 20cm. Jak dobrać wymiary walca aby pole jego powierzchni
bocznej było największe

(fajnie jakby ktoś mógł to również narysować=>łatwiej zrozumieć)
2.) Przekrój osiowy stożka ma obwód 30cm. Czy można dobrać tak wymiary stożka aby jego pole
powierzchni bocznej było największe?
3.)Okno ma kształt prostokąta zakończonego na górze półkolem.Jaka powinna być podstawa
prostokąta aby przy obwodzie okna wynoszącym 2m powierzchnia okna była największa

22 cze 14:30
magda:
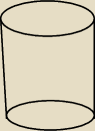
to jest walec

22 cze 14:39
magda:
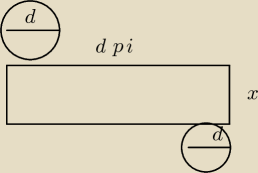
przekros osiowy walca
22 cze 14:41
magda: sory zle podpisalam to jest siatka

22 cze 14:41
magda:

a to owy przekroj osiowy

22 cze 14:42
magda: Pb(x)=πx*x
Pb(x)=πx
2
obw=2x+2d
obw=20cm

x+d=10
d=10−x
22 cze 14:44
magda: Pb=πdx
Pb=π(10−x)x
Pb=10πx−πx2
pb=−πx(x−10)
x1=0 x2=10
22 cze 14:46
magda: Punkt x gdzie największy jest y możemy policzyć poprzez średnią arytmetyczną:
(x1+x2)/2
(0+10)/2
10/2=5
x=5cm
d=10−x=10−5=5 cm
d=x=5cm
Pb=3.14*d*x
Pb=3.14*5*5
Pb=78.53cm2
22 cze 14:47
magda: Dziedzina:
Nasz x musi być większy od 0 ale jednocześnie mniejszy od 10, ponieważ obwód przekroju osiowego
tego walca ma wynosić 20 cm. Z tego wynika że:
x>0
x<10 d="<0,10">
Odp. Największe pole powierzchni bocznej będzie gdy d=5 cm i x=5 cm gdyż pole będzie wynosiło
78.53cm2.
22 cze 14:48
Wydi: No dzięki wystarczyło sam przekrój osiowy...

wiem jak wygląda walec

22 cze 14:48
magda: a tak na chlopski rozum

Ob=20
Boki:
a
b=10−a
Pole:
10a−a2
p=−b/2a
−10/−2=5
a=5
b=5
P=5*5 + (5 (pierwiastek)3/4)*4=25+5(pierwiastek)3
22 cze 14:49
Wydi: OK

22 cze 14:49
Wydi: A kolejne zadanka?
22 cze 15:07
Bogdan:

d − długość średnicy walca, P − pole powierzchni bocznej, H − wysokość walca.
2πd + 2H = 20 ⇒ H = 10 − πd
P = πd * H → max
P = πd(10 − πd) ⇒ P(d) = −π
2d
2 + 10πd
Funkcja P(d) jest funkcją kwadratową, której wykresem jest parabola skierowana ramionami
| | −10π | | 5 | |
w dół i posiadającą maksimum dla d = |
| = |
| . |
| | −2π2 | | π | |
Odp.: Pole powierzchni bocznej walca, którego przekrój osiowy ma obwód 20 jest największe
22 cze 15:19
magda: Bogdan a po co 2 razy to samo?
22 cze 15:20
Bogdan:
Nie jest to samo. Pokazałem poprawny zapis rozwiązania zadania optymalizacyjnego.
Należy w zapisie rozwiązania wyraźnie stwierdzić, że otrzymano funkcję kwadratową,
która posiada maksimum lub minimum (w zależności od treści zadania) uzasadniając
w ten sposób rozwiązanie. Nie ma potrzeby wyznaczać miejsc zerowych otrzymanej
funkcji kwadratowej.
22 cze 15:31
Wydi: Dziękuje Bogdanie

22 cze 15:52
magda: spoko ucze sie jeszcze

22 cze 19:14
 (fajnie jakby ktoś mógł to również narysować=>łatwiej zrozumieć)
2.) Przekrój osiowy stożka ma obwód 30cm. Czy można dobrać tak wymiary stożka aby jego pole
powierzchni bocznej było największe?
3.)Okno ma kształt prostokąta zakończonego na górze półkolem.Jaka powinna być podstawa
prostokąta aby przy obwodzie okna wynoszącym 2m powierzchnia okna była największa
(fajnie jakby ktoś mógł to również narysować=>łatwiej zrozumieć)
2.) Przekrój osiowy stożka ma obwód 30cm. Czy można dobrać tak wymiary stożka aby jego pole
powierzchni bocznej było największe?
3.)Okno ma kształt prostokąta zakończonego na górze półkolem.Jaka powinna być podstawa
prostokąta aby przy obwodzie okna wynoszącym 2m powierzchnia okna była największa
 to jest walec
to jest walec
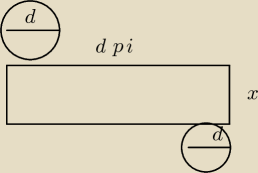 przekros osiowy walca
przekros osiowy walca

 a to owy przekroj osiowy
a to owy przekroj osiowy
 x+d=10
d=10−x
x+d=10
d=10−x
 wiem jak wygląda walec
wiem jak wygląda walec
 Ob=20
Boki:
a
b=10−a
Pole:
10a−a2
p=−b/2a
−10/−2=5
a=5
b=5
P=5*5 + (5 (pierwiastek)3/4)*4=25+5(pierwiastek)3
Ob=20
Boki:
a
b=10−a
Pole:
10a−a2
p=−b/2a
−10/−2=5
a=5
b=5
P=5*5 + (5 (pierwiastek)3/4)*4=25+5(pierwiastek)3

 d − długość średnicy walca, P − pole powierzchni bocznej, H − wysokość walca.
2πd + 2H = 20 ⇒ H = 10 − πd
P = πd * H → max
P = πd(10 − πd) ⇒ P(d) = −π2d2 + 10πd
Funkcja P(d) jest funkcją kwadratową, której wykresem jest parabola skierowana ramionami
d − długość średnicy walca, P − pole powierzchni bocznej, H − wysokość walca.
2πd + 2H = 20 ⇒ H = 10 − πd
P = πd * H → max
P = πd(10 − πd) ⇒ P(d) = −π2d2 + 10πd
Funkcja P(d) jest funkcją kwadratową, której wykresem jest parabola skierowana ramionami

