okrąg
basia: dany jest okrąg o równaniu x
2 − 16x + y
2 = 0. Wykaż, ze zbiór wszystkich
środków cięciw tego okręgu poprowadzonych z początku układu współrzędnych jest okręgiem o
środku S=(4,0) i promieniu r= 4.
wyznaczyłam równanie prostej zawierającej cięciwę (y= ax) i nie wiem co dalej
POMOOOCY
Patronus:
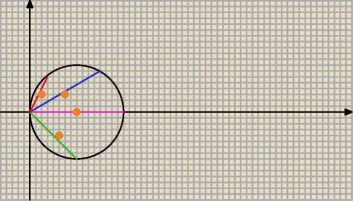
Mamy okrąg (x−8)
2 + y
2 = 64, o środku w punkcie (8,0) i promieniu 8.
Środki cięciw to odległość od punktu (0,0) do końca okręgu podzielona na 2
Zatem:
y
2 = −x
2 + 16x
y =
√−x2 + 16x
O = (0,0). B = (x,
√−x2 + 16x)
|OB|/2 = f(x) =
√(x−0)2 + (√−x2 + 16x − 0)2 :2 =
√x2 + |− x2+16x| :2
f(x) = y =
√x2 + |− x2+16x| :2
y
2 = |x
2 + |−x
2 + 16x||:4
I coś mi nie wychodzi
Ale ogólny sens jest właśnie taki, może znajdziesz gdzieś błąd