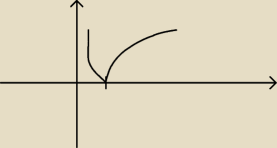
funkcje kartofelek: nie rozumiem dlaczego f: R/{1} −> R f(x)=log I x−1I jest odwzorowaniem "na" ? Przecież to wygląda mw tak: czyli dla x c R\{1} y będzie zawsze (o, + nieskończoności). Więc dlaczego w odpowiedziach jest, że jest to odwzorowanie "na" ?

kartofelek: proszę o pomoc, to krótkie pytanie

kartofelek: ponawiam prośbę

PW: y=log|x−1| ⇔ 10^y=|x−1| Ostatnie równanie z niewiadomą y ma rozwiązanie dla każdego x≠1 (wystarczy narysować wykres funkcji 10^y − jak wiadomo jest to funkcja przyjmująca wszystkie wartości nieujemne, a |x−1| jest liczbą nieujemną). Albo prościej: masz zły wykres. Trzeba to sobie uzmysłowić tak: dla x>1 f(x) = log (x−1) Wykres tej funkcji to wykres funkcji g(x) = logx, przesunięty o wektor [1.0] . Tak jak wykres g miał pionową asymptotę x=0, tak wykres funkcji f ma pionową asymptotę x=1. Narysowanie wykresu dla x> 1 już kończy sprawę − niezależnie od tego jaki jest wykres dla x<1, już mamy odwzorowanie "na" osiągane są wszystkie wartości rzeczywiste. Nie ma potrzeby rysowania wykresu dla x<1, ale gdybyś chciał być skrupulatny, to trzeba narysować drugą połówkę wykresu − symetryczną do tej pierwszej względem osi x=1.