Punkt należy do okręgu lubielubielubie: Spośród punktów (x,y) gdzie x należy (1,2,3,4,5) oraz y (1,2,3 ) wybrano losowo jeden punkt. Jakie jest prawdopodobieństwo że wylosowany punkt należy do okręgu o równaniu x2 + y2 − 6x − 4y + 12 = 0 ?

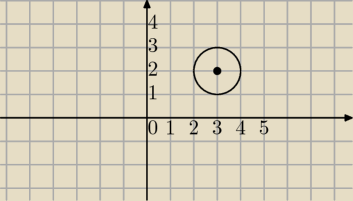
Mila: x² + y² − 6x − 4y + 12 = 0 do postaci kanonicznej (x−3)²−9+(y−2)²−4+12=0 (x−3)²+(y−2)²=1² Skorzystaj z rysunku jakie punkty kratowe nalezą do tego okręgu? Czy mogą być wylosowane? Ω=5*3=15

Skipper: ... no własnie Miła Milu ... czy napewno ?

Skipper: ... skoro Ω to zbiór wszystkich jednakowo prawdopodobnych zdarzeń elememtarnych Na okręgu nie leżą żadne punkty o współrzędnej x−owej 1 lub 5 ... czy są więc to zdarzenia jednakowo prawdopodobne ?−