geometria Ada: ddany jest odcinek o koncach a=(1,2) i b=(−1,−4). funkcja f przyporzadkowuje odcietej dowolnego punktu P nalezacego do odcinka AB odleglosc |PR| , gdzie R=(0,1). wyznacz wzor, zbior wartosci i wartosc najmniejsza funkcji f. witam mozecie mi wyjasnic o co wlasciwie pytaja sie w tym zadaniu ?

Ada: help

dumka: najpierw musisz zrobic wzór na funkcję potem narysowac w ukłądize i zaznaczyc punkt

Ada: no wiesz niewiele mi to mowi pozatym ta funkcja jest jakas dziwna bo ja to rozumiem tak ze odleglosc punktu p od r jest wartoscia tej funcji wiec f min powinno byc w odleglosci RA a tak nie jest....

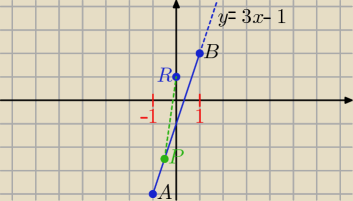
Bogdan: Prosta zawierająca punkty A, B określona jest wzorem (trzeba ten wzór wyznaczyć) y = 3x − 1. Każdy punkt na tej prostej ma współrzędne (x, 3x − 1), a więc współrzędne punktu P=(x, 3x − 1) dla x∊<−1, 1>. |PR| = √ (x − 0)² + (3x − 1 − 1)² = √ 10x² − 12x + 4 Każdej argumentowi x∊<−1, 1> funkcji f(x) przyporządkowana jest wartość √ 10x² − 12x + 4 , czyli f(x) = √ 10x² − 12x + 4

Bogdan: Każdemu argumentowi ...

Bogdan: I co Ty na to Ado?

Ada: no teraz kumam )