geometria analityczna Hej :): Narysuj w układzie współrzędnych zbiór punktów, których współrzędne spełniają nierówność: |x − 2| + 2|y| ≤ 5 Zapisałam to w postaci alternatywy warunków:

⎧	x≥2
⎨	y≥0
⎩	x − 2 + 2y ≤ 5

	⎧	x<2
∨	⎨	y≥0
	⎩	−x + 2 + 2y ≤5

	⎧	x<2
⋁	⎨	y<0
	⎩	−x + 2 − 2y ≤5

	⎧	x≥2
∨	⎨	y<0
	⎩	x − 2 − 2y ≤5

i nie wiem jak to narysować próbowałam przerobić to tak aby przypominało wzór funkcji liniowej, ale nie chce mi wyjść takie rozwiązanie jakie jest w odpowiedziach Czy jest ktoś kto mógłby mi wytłumaczyć jak to narysować ?

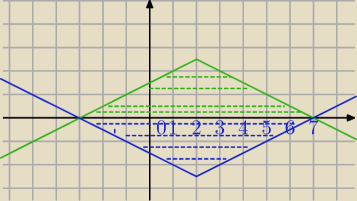Mila: |x − 2| + 2|y| ≤ 5⇔ 2|y|≤−|x−2|+5⇔

	1
|y|≤−		|x−2|+2,5
	2

1) y≥0 rozpatrujesz punkty nad osią OX

	1		1
y≤−		|x−2|+2,5 punkty I i II ćwiartki leżące pod wykresem y=−		|x−2|+2,5 (zielony)
	2		2

2) y<0 |y|=−y

	1
−y≤−		|x−2|+2,5⇔
	2

	1		1
y≥		|x−2|−2,5 punkty III i IV ćwiartki leżące nad wykresem y=		|x−2|−2,5
	2		2

krystek: @Mila pozdrawiam i zobacz zad Rotarci . Jestem w domu zdrowa,

Mila: Witaj, Krytek. Napisałam komentarz. Pozdrawiam.

Hej :): Dzięki

Mila: