Wyznacz ekstrema lokalne. Martyna: f(x)=³√(x²−1)²

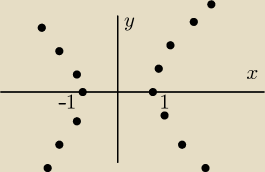
AS: Dziedzina: x² − 1 > 0 ⇔ x ≤ −1 lub x ≥ 1 f(x) = (x² −1 )^2/3 f'(x) = 2/3*(x² −1)^{2/3 − 1}*2*x = 2/3*(x² − 1)^−1/3*2*x f'(x) = 0 ⇔ 2*x = 0 ⇔ x = 0 ale x = 0 nie należy do dziedziny. Brak ekstremum.

Bogdan: Asie ?

AS: Wyraźniej! O co chodzi?

Eta: AS .... D= R

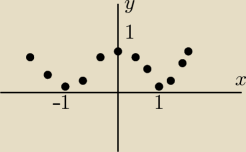
AS: Ale wpadka! Niech się spalę ze wstydu! Anuluję moje rozwiązanie! f(x) = ³√(x² − 1)² Dziedzina: R f'(x) = 1/3*((x² − 1)²)^{1/3 − 1}*2*(x² − 1)*2*x = 1/3*((x² − 1)²)^−2/3*4*x*(x² − 1) f'(x) = 0 ⇔ x = −1 lub x = 0 lub x = 1 x −1 0 1 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− f'(x) − 0 + 0 − 0 + f(x) 0 1 0 min max min

AS: Do Ety Dziękuję

Eta: Jaka wpadka? .... zdarza sie najlepszym ( zapewne miałeś na uwadze pierwiastek kwadratowy.) teraz jest OK! napisałabym jeszcze max lokalne

Bogdan: Proszę sprawdzić pochodną funkcji f(x) = (x² − 1)^2/3

Bogdan: ... oraz wyznaczyć dziedzinę pochodnej.

Eta: Bogdanie .. nie spojrzałam na pochodną obliczoną przez AS oczywiście :

	4x
f'(x) =		..... co zmienia postać rzeczy!
	33√x2 −1

Eta: D^' = R − { −1, 1}

Eta: Najwyraźniej AS zdenerwował się obliczeniem dziedziny w pierwszej wersji AS....... dawaj zatem poprawne rozwiązanie! PS: ''wyprowadziłeś " i mnie w pole ( zaufałam Ci w poprawności obliczenia pochodnej)

Bogdan: Co wcale nie znaczy, że w punktach x = −1, x = 1 nie istnieje ekstremum funkcji, funkcja w tych punktach jest określona.

Eta: Oczywiście !....czekam na prawidłowe rozwiązanie przez AS

AS: f(x) = ³√(x² − 1)² Dziedzina: R Funkcja f(x) osiągnie ekstremum gdy funkcja g(x) = (x² − 1)² osiągnie ekstremum. Pochodna funkcji g(x) g'(x) = 2*(x² − 1)*2*x = 4*(x + 1)*x*(x − 1) g'(x) = 0 ⇔ x = −1 lub x = 0 lub x = 1 x −1 0 1 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− g'(x) − 0 + 0 − 0 + −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− g(x) min max min Oto pochodna funkcji f(x) − skoro męczydusza tak nalega. Zgadzam się − każdą robotę należy robić dobrze i do końca. f(x) = ³√u² = u^2/3 gdzie u = x² − 1 f'(x) = 2/3*u^{2/3 − 1}*u" = 2/3*u^−1/3*u' gdzie u' = 2*x f'(x) = 4*x/(3*³√x² − 1) Dziedzina dla pochodnej: x < −1 lub x > 1 Uff − chyba teraz już wszystko dobrze. Bo jak nie to się powieszę (oczywiście na szyi dorodnej pani)

Bogdan: Dzień dobry. Ja też lubię takie wieszanie się. Jaka jest Asie dziedzina pochodnej funkcji?, podałeś: x < −1 lub x > 1.

AS: Przyjdzie mi się jednak powiesić. Oczywiście x ≠ ± 1 , przyjąłem oczywiście pierwiastek st.2−go a jest st.3 −go Uff ta skleroza.

Miś:

tim: Miś

tim: